题目内容
18、如图，已知梯形ABCD，AD∥BC，AD=DC=4，BC=8，点N在BC上，CN=2，E是AB中点，在AC上找一点M使EM+MN的值最小，此时其最小值等于6
．分析：首先找N关于AC的对称点N′，然后根据轴对称的性质进行计算．
解答：解：∵AD=DC
∴∠DCA=∠DAC=∠ACB，
AC平分∠BCD
N关于AC的对称点N′，CN′=2
所以N′为CD中点所以EN′∥AD
M为EN′与AC的交点则MN=MN′，
此时EM+MN最小最小值=EN′=（4+8）÷2=6．
∴∠DCA=∠DAC=∠ACB，
AC平分∠BCD
N关于AC的对称点N′，CN′=2
所以N′为CD中点所以EN′∥AD
M为EN′与AC的交点则MN=MN′，
此时EM+MN最小最小值=EN′=（4+8）÷2=6．
点评：此题主要考查有关轴对称--最短路线的问题，作N关于AC的对称点N′是关键．
练习册系列答案
阅读快车系列答案
相关题目
9、如图，已知梯形ABCD中，AD∥BC，BE平分∠ABC，BE⊥CD，∠A=110°，AD=3，AB=5，则BC的长为（ ）
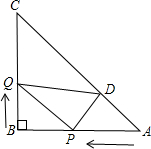点到达终点时，另一点也随之停止．过Q作QD∥AB交AC于点D，连接PD，设运动时间为t秒时，四边形BQDP的面积为s．
（2007•遂宁）如图，已知等腰△ABC的面积为4cm2，点D、E分别是AB、AC边的中点，则梯形DBCE的面积为