题目内容
通过观察发现方程x+| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x+1 |
| 1 |
| b+1 |
分析:根据所给出的方程和解,可以发现方程x+
=b+
可以变形为x+1+
=b+1+
,从而得出方程x+
=b+
的解即可.
| 1 |
| x+1 |
| 1 |
| b+1 |
| 1 |
| x+1 |
| 1 |
| b+1 |
| 1 |
| x+1 |
| 1 |
| b+1 |
解答:解:∵方程x+
=2+
的解是x=2或x=
;x+
=3+
的解x=3或x=
;
∴方程x+
=b+
可以变形为x+1+
=b+1+
,
当未知数为x+1时,解为b+1与
,从而得出x的值.
即x1=b,x2=
-1=-
.
故答案为x1=b,x2=-
.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
∴方程x+
| 1 |
| x+1 |
| 1 |
| b+1 |
| 1 |
| x+1 |
| 1 |
| b+1 |
当未知数为x+1时,解为b+1与
| 1 |
| b+1 |
即x1=b,x2=
| 1 |
| b+1 |
| b |
| b+1 |
故答案为x1=b,x2=-
| b |
| b+1 |
点评:本题是一道找规律的题目,考查了分式方程的解法,注意整体思想的运用.

练习册系列答案
相关题目
通过观察发现方程x+
=2+
的解是x1=2或x2=
;x+
=3+
的解是x1=3或x2=
;按照你发现的规律,则方程x+
=b+
的解是( )
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x+1 |
| 1 |
| b+1 |
A、x1=b或x2=
| ||
B、x1=b或x2=
| ||
C、x1=b+1或x2=
| ||
D、x1=b或x2=-
|
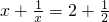 的解是
的解是 ;
;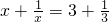 的解是
的解是 ;按照你发现的规律,则方程
;按照你发现的规律,则方程 的解是
的解是



 ;
; ;按照你发现的规律,则方程
;按照你发现的规律,则方程