题目内容
 (2012•南安市质检)如图,已知双曲线y=
(2012•南安市质检)如图,已知双曲线y=| k-3 |
| x |
| k-3 |
| x |
(1)若直线l的解析式为y=
| 1 |
| 6 |
①求a、k的值;②当AM=2MP时,求点P的坐标.
(2)若AM=m•MP,BM=n•MQ,求m-n的值.
分析:(1)①由A(a,1)在直线y=
x上,得
a=1,解得a=6,然后根据A(6,1)在双曲线y=
上解得k=9;
②过点A作AE⊥y轴于E,过点M作MF⊥y轴于F得到MF∥AE后即可证明△PMF∽△PAE,利用相似三角形对应线段的比相等得到MF=2,从而得到点M(2,3),利用待定系数法求得直线AM的解析式即可;
(2)如图,设点A的横坐标为b,点M的横坐标为t,则点B的横坐标为-b;过点B作BC⊥y轴于C,过点M作MD⊥AE于D,根据MD∥y轴得到△AMD∽△APE根据相似三角形对应线段的比相等用b、t表示出m和n,从而求得m-n的值.
| 1 |
| 6 |
| 1 |
| 6 |
| k-3 |
| x |
②过点A作AE⊥y轴于E,过点M作MF⊥y轴于F得到MF∥AE后即可证明△PMF∽△PAE,利用相似三角形对应线段的比相等得到MF=2,从而得到点M(2,3),利用待定系数法求得直线AM的解析式即可;
(2)如图,设点A的横坐标为b,点M的横坐标为t,则点B的横坐标为-b;过点B作BC⊥y轴于C,过点M作MD⊥AE于D,根据MD∥y轴得到△AMD∽△APE根据相似三角形对应线段的比相等用b、t表示出m和n,从而求得m-n的值.
解答:解:(1)①∵A(a,1)在直线y=
x上,
∴
a=1,
解得a=6
∵A(6,1)在双曲线y=
上,
∴
=1,
解得k=9
②如图,过点A作AE⊥y轴于E,过点M作MF⊥y轴于F,
则MF∥AE,
则△PMF∽△PAE,
则
=
,即
=
,
解得MF=2
则Mx=2,则My=
=3,
则点M(2,3)
∵A(6,1)、M(2,3),
∴直线AM的解析式为y=-
x+4.
∴点P(0,4)
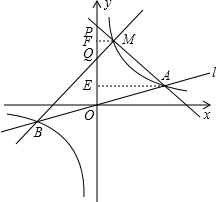
(2)如图,设点A的横坐标为b,点M的横坐标为t,则点B的横坐标为-b;
过点B作BC⊥y轴于C,过点M作MD⊥AE于D,
∵MD∥y轴,
∴△AMD∽△APE,
∴
=
,即
=
,得m=
①
∵MF∥BC,
∴△MFQ∽△BCQ,
∴
=
,即
=
,得n=
∴m-n=
-
=-2

| 1 |
| 6 |
∴
| 1 |
| 6 |
解得a=6
∵A(6,1)在双曲线y=
| k-3 |
| x |
∴
| k-3 |
| 6 |
解得k=9
②如图,过点A作AE⊥y轴于E,过点M作MF⊥y轴于F,
则MF∥AE,
则△PMF∽△PAE,
则
| MF |
| AE |
| PM |
| PA |
| MF |
| 6 |
| 1 |
| 3 |
解得MF=2
则Mx=2,则My=
| 6 |
| 2 |
则点M(2,3)
∵A(6,1)、M(2,3),
∴直线AM的解析式为y=-
| 1 |
| 2 |
∴点P(0,4)

(2)如图,设点A的横坐标为b,点M的横坐标为t,则点B的横坐标为-b;
过点B作BC⊥y轴于C,过点M作MD⊥AE于D,
∵MD∥y轴,
∴△AMD∽△APE,
∴
| AM |
| AP |
| AD |
| AE |
| m |
| m+1 |
| b-t |
| b |
| b-t |
| t |
∵MF∥BC,
∴△MFQ∽△BCQ,
∴
| FM |
| BC |
| MQ |
| BQ |
| t |
| b |
| 1 |
| n-1 |
| b+t |
| t |
∴m-n=
| b-t |
| t |
| b+t |
| t |

点评:此题综合考查了反比例函数,正比例函数等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
相关题目
 (2012•南安市质检)已知二次函数y=x2+bx-3(b为常数)的图象经过点(2,-3 ).
(2012•南安市质检)已知二次函数y=x2+bx-3(b为常数)的图象经过点(2,-3 ). (2012•南安市质检)(1)计算:6x3÷2x=
(2012•南安市质检)(1)计算:6x3÷2x=