题目内容
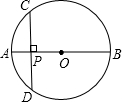 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为________cm.
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为________cm.
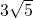
分析:要求⊙O的半径,只要连接OC,在Rt△PCO中根据勾股定理就可以得到.
解答:
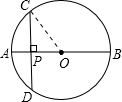 解:连接OC,
解:连接OC,设AP=x,则PB=5x,
∴OP=3x-x=2x.
∵CD⊥AB,∴PC=
 CD=
CD= ×10=5.
×10=5.在Rt△PCO中,OC2-OP2=PC2,
∴(3x)2-(2x)2=52,
∴x=
 ,∴⊙O的半径为3
,∴⊙O的半径为3 cm.
cm.点评:此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.

练习册系列答案
相关题目
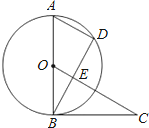 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.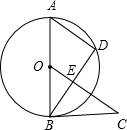 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.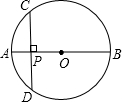 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为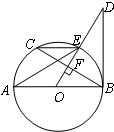 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )