题目内容
同一平面内相交于一点的三条直线最多能构成( )对对顶角.
| A、4 | B、5 | C、6 | D、7 |
考点:对顶角、邻补角
专题:
分析:三条直线相交于一点可看成是三种两条直线相交于一点的情况,所以形成6对对顶角.
解答:解:∵三条直线相交于一点可看成是三种两条直线相交于一点的情况,
两条直线相交于一点有两对对顶角,
∴同一平面内相交于一点的三条直线形成2×3=6对对顶角.
故答案为:6.
两条直线相交于一点有两对对顶角,
∴同一平面内相交于一点的三条直线形成2×3=6对对顶角.
故答案为:6.
点评:本题考查了对顶角的概念,把三条直线相交于一点可看成是三种两条直线相交于一点的情况,是解题的关键.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
下列语句正确的是( )
| A、连接两点的线段叫做两点间的距离 |
| B、两条直线平行,对顶角相等 |
| C、如果两个角互补,那么这两个角为邻补角 |
| D、平移变换中,各组对应点连成的线段平行且相等 |
若2是关于方程x2-5x+c=0的一个根,则这个方程的另一个根是( )
| A、-3 | B、3 | C、-6 | D、6 |
方程组
的解与x与y的值相等,则k等于( )
|
| A、1 | B、-1 | C、2 | D、-2 |
一条直线y=kx+b其中k+b=-6,kb=8,那么该直线经过( )
| A、第二、四象限 |
| B、第一、二、三象限 |
| C、第一、三象限 |
| D、第二、三、四象限 |
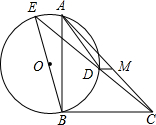 如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=
如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=