题目内容
以线段a=13，b=13，c=10，d=6为边作梯形，其中a，c为梯形的两底，这样的梯形
- A.能作一个
- B.能作两个
- C.能作无数个
- D.一个也不能作
D
分析：过点B作BE∥AD，则出现?ABED和一个△BEC，此外的关键是根据已知求得CE的长，然后判断BE，CE，BC是否能构成三角形，能构成则能做一个梯形，否则不能做一个梯形．
解答：
解：如图，过点B作BE∥AD，则出现?ABED和一个△BEC
∵AB=10，CD=13，AD=13，BC=6
∴CE=3，BE=13
∵3+6＜13
∴BE，CE，BC不能构成三角形
∴这样的梯形一个也不能作，
故选D．
点评：此题主要考查平行四边形的判定与性质及三角形三边关系的综合运用，关键是利用三角形三边关系判定是否能构成三角形．
分析：过点B作BE∥AD，则出现?ABED和一个△BEC，此外的关键是根据已知求得CE的长，然后判断BE，CE，BC是否能构成三角形，能构成则能做一个梯形，否则不能做一个梯形．
解答：
解：如图，过点B作BE∥AD，则出现?ABED和一个△BEC∵AB=10，CD=13，AD=13，BC=6
∴CE=3，BE=13
∵3+6＜13
∴BE，CE，BC不能构成三角形
∴这样的梯形一个也不能作，
故选D．
点评：此题主要考查平行四边形的判定与性质及三角形三边关系的综合运用，关键是利用三角形三边关系判定是否能构成三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
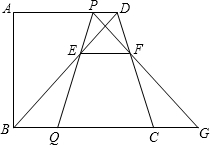P、Q分别在边AD和BC上，且BQ=2DP．线段PQ与BD相交于点E，过点E作EF∥BC，交CD于点F，射线PF交BC的延长线于点G，设DP=x．