题目内容
(1)sin30°=
.
(2)已知方程:x2-1=0,则x=
| 1 |
| 2 |
| 1 |
| 2 |
(2)已知方程:x2-1=0,则x=
±1
±1
.分析:(1)根据特殊角的三角函数值可以直接得到答案;
(2)首先把-1移到方程右边,再两边直接开平方即可.
(2)首先把-1移到方程右边,再两边直接开平方即可.
解答:解:(1)sin30°=
;
(2)x2-1=0,
移项得:x2=1,
两边直接开平方得:x=±1.
故答案为:
;±1.
| 1 |
| 2 |
(2)x2-1=0,
移项得:x2=1,
两边直接开平方得:x=±1.
故答案为:
| 1 |
| 2 |
点评:此题主要考查了特殊角的三角函数,一元二次方程的解法,解这类问题要移项,把所含未知数的项移到等号的左边,把常数项移项等号的右边,化成x2=a(a≥0)的形式,利用数的开方直接求解.

练习册系列答案
相关题目
实数
,sin30°,
+1,2π,(
)0,|-3|中,有理数的个数是( )
| 22 |
| 7 |
| 2 |
| 3 |
| A、2个 | B、3个 | C、4个 | D、5个 |
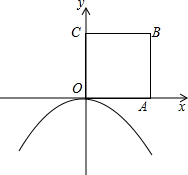 如图所示,边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕点O顺时针旋转30°,使点A落在抛物线y=ax2(a<0)的图象上.
如图所示,边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕点O顺时针旋转30°,使点A落在抛物线y=ax2(a<0)的图象上.