题目内容
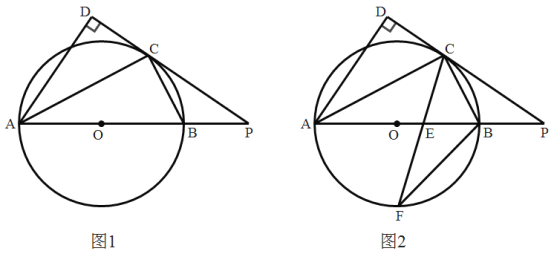
【题目】如图,![]() 是
是![]() 的外接圆,AB为
的外接圆,AB为![]() 的直径,在
的直径,在![]() 外侧作
外侧作![]() ,过点C作
,过点C作![]() 于点D,交AB延长线于点P.
于点D,交AB延长线于点P.
(1)求证:PC是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;(用含m的代数式表示)
的半径;(用含m的代数式表示)
(3)如图2,在(2)的条件下,作弦CF平分![]() ,交AB于点E,连接BF,且
,交AB于点E,连接BF,且![]() ,求线段PE的长.
,求线段PE的长.
【答案】:(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接OC,根据平行线的判定可得![]() ,从而得出
,从而得出![]() ,然后根据切线的判定定理即可证出PC是
,然后根据切线的判定定理即可证出PC是![]() 的切线;
的切线;
(2)根据直径所对的圆周角是直角可得:∠ACB=90°,然后根据同角的余角相等相等可得![]() ,然后根据锐角三角函数可得
,然后根据锐角三角函数可得![]() ,
,![]() ,根据勾股定理可得:
,根据勾股定理可得:![]() ,结合已知条件即可求出BC,从而求出AB,即可求出圆的半径;
,结合已知条件即可求出BC,从而求出AB,即可求出圆的半径;
(3)连接AF,OC,过C作![]() ,根据等腰三角形的判定及性质即可求出AB=10,从而求出BC、OC和AC,利用锐角三角函数即可求出CF,再根据相似三角形的判定及性质可求出EF和CE,从而求出CG、OG,根据射影定理可求出OP,然后根据勾股定理可求出EG,从而求出OE的长,即可求出线段PE的长.
,根据等腰三角形的判定及性质即可求出AB=10,从而求出BC、OC和AC,利用锐角三角函数即可求出CF,再根据相似三角形的判定及性质可求出EF和CE,从而求出CG、OG,根据射影定理可求出OP,然后根据勾股定理可求出EG,从而求出OE的长,即可求出线段PE的长.
解析:(1)如图,连接OC
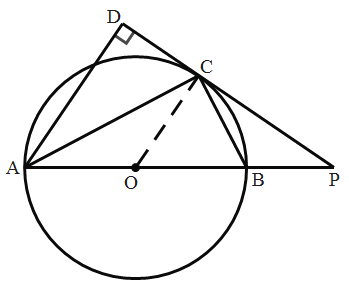
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
即PC为![]() 的切线;
的切线;
(2)∵AB为直径
∴∠ACB=90°
∵∠BCP+∠ACD=180°-∠ACB=90°
∵∠DAC+∠ACD=90°
∴![]()
∴![]()
则![]() ,
,![]()
根据勾股定理:![]()
![]()
∴![]()
又∵![]()
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,
∴半径为![]()
(3)如图,连接AF,OC,过C作![]()
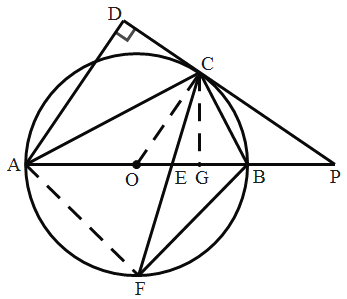
∵![]() ,
,![]()
∴![]()
∴![]()
又∵![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
∵![]()
∴![]() ,
,
∴![]() ,
,![]() ,
,![]()
如下图,在![]() 中
中
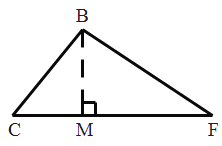
过B作![]()
∵![]()
∴![]()
又∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
又∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
即![]()
![]() 中,
中,![]() ,
,![]()
解得:CG=4
则在![]() 中,
中,![]() ,
,![]() ,
,![]()
根据勾股定理可得:OG=![]()
由射影定理,![]()
∴![]()
又∵![]() ,
,![]()
∴![]() ,且
,且![]()
∴![]()
∴![]()

练习册系列答案
相关题目