题目内容
9.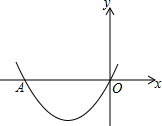 如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.
如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.
分析 首先求出抛物线的顶点坐标以及AO的长,再利用平移的性质结合AO只是左右平移,进而得出旋转的角度.
解答 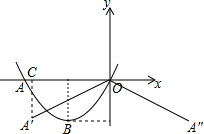 解:由题意可得:y=$\frac{1}{2}{x^2}$+2x=$\frac{1}{2}$(x+2)2-2,
解:由题意可得:y=$\frac{1}{2}{x^2}$+2x=$\frac{1}{2}$(x+2)2-2,
故抛物线的顶点坐标为:(-2,-2),
当y=0时,0=$\frac{1}{2}$(x+2)2-2
解得:x1=0,x2=4,
故AO=4,
∵将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,
∴旋转后对应点A′到x轴的距离为:2,
如图,过点A′作A′C⊥x轴于点C,
当∠COA′=30°,
则CA′=$\frac{1}{2}$A′O=2,
故α为30°时符合题意,
同理可得:α为150°时也符合题意,
综上所述:所有符合题意的α的值是30°或150°.
故答案为:30°或150°.
点评 此题主要考查了抛物线与x轴的交点以及旋转与平移变换,正确得出对应点的特点是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.计算($\sqrt{2}$+1)2016•($\sqrt{2}$-1)2015的结果是( )
| A. | 1 | B. | -1 | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$-1 |
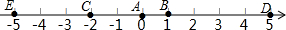 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.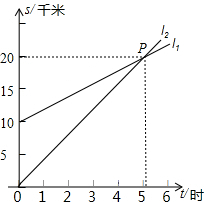 如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空: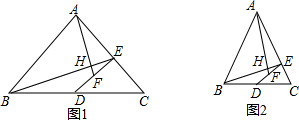




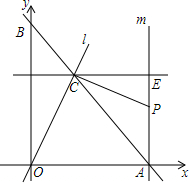 如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.
如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.