题目内容
17. 如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )
如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )| A. | 4cm2 | B. | 6cm2 | C. | 8cm2 | D. | 9cm2 |
分析 取CG的中点H,连接EH,根据三角形的中位线定理可得EH∥AD,再根据两直线平行,内错角相等可得∠GDF=∠HEF,然后利用“角边角”证明△DFG和△EFH全等,根据全等三角形对应边相等可得FG=FH,全等三角形的面积相等可得S△EFH=S△DGF,再求出FC=3FH,再根据等高的三角形的面积比等于底边的比求出两三角形的面积的比,从而得解.
解答 解:如图,取CG的中点H,连接EH,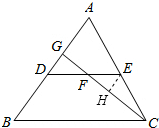
∵E是AC的中点,
∴EH是△ACG的中位线,
∴EH∥AD,
∴∠GDF=∠HEF,
∵F是DE的中点,
∴DF=EF,
在△DFG和△EFH中,$\left\{\begin{array}{l}{∠GDF=∠HEF}&{\;}\\{DF=EF}&{\;}\\{∠DFG=∠EFH}&{\;}\end{array}\right.$,
∴△DFG≌△EFH(ASA),
∴FG=FH,S△EFH=S△DGF,
又∵FC=FH+HC=FH+GH=FH+FG+FH=3FH,
∴S△CEF=3S△EFH,
∴S△CEF=3S△DGF,
∴S△DGF=$\frac{1}{3}$×12=4(cm2).
故选:A.
点评 本题考查了三角形的中位线定理,全等三角形的判定与性质,作辅助线,利用三角形的中位线进行解题是解题的关键.

练习册系列答案
相关题目
2.某服装店用7000元购进A、B两种新式服装,按标价售出后获得毛利润4000元(毛利润=售价-进价),这两种服装的进价,标价如表所示:
求这两种服装各购进的件数?
| 类型 价格 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 150 |
6. 如图,数轴上点A所表示的数的相反数的倒数是( )
如图,数轴上点A所表示的数的相反数的倒数是( )
 如图,数轴上点A所表示的数的相反数的倒数是( )
如图,数轴上点A所表示的数的相反数的倒数是( )| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN长的最大值是5$\sqrt{2}$.
如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN长的最大值是5$\sqrt{2}$. 如图,等边△ABC的边长为2,小亮建立了如图所示的坐标系,此时顶点A的坐标为(-1,$\sqrt{3}$).
如图,等边△ABC的边长为2,小亮建立了如图所示的坐标系,此时顶点A的坐标为(-1,$\sqrt{3}$). 如图,△BDC与△CEB在线段BC的同侧,CD与BE相交于点A,∠ABC=∠ACB,AD=AE,求证:BD=CE.
如图,△BDC与△CEB在线段BC的同侧,CD与BE相交于点A,∠ABC=∠ACB,AD=AE,求证:BD=CE.