题目内容
 如图,在五边形ABCDE中,AB=BC,N为BC延长线上一点,过N作∠ANM=∠ABC=∠BCD,交∠BCD的外角平分线于M,试问AN=NM成立吗?
如图,在五边形ABCDE中,AB=BC,N为BC延长线上一点,过N作∠ANM=∠ABC=∠BCD,交∠BCD的外角平分线于M,试问AN=NM成立吗?考点:四点共圆,三角形内角和定理,等腰三角形的判定与性质,圆周角定理,圆内接四边形的性质
专题:证明题
分析:连接AC、AM,易证∠BAC=∠BCA=∠NCM=∠DCM,从而得到∠ACM=∠BCD=∠ANM,进而得到A、C、N、M四点共圆,然后根据圆周角定理可得∠NAM=∠NCM,根据圆内接四边形的性质可得∠BCA=∠NMA,就可得到∠NMA=∠NAM,从而有AN=NM.
解答:答:AN=NM成立
证明:连接AC、AM,如图.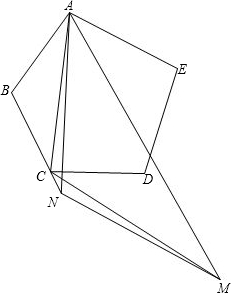
∵AB=BC,
∴∠BAC=∠BCA,
∴∠BAC=∠BCA=
.
∵CM平分∠NCD,
∴∠NCM=∠DCM,
∴∠NCM=∠DCM=
.
∵∠ANM=∠ABC=∠BCD,
∴∠BAC=∠BCA=∠NCM=∠DCM,
∴∠ACM=∠ACD+∠DCM=∠ACD+∠BCA=∠BCD=∠ANM,
∴A、C、N、M四点共圆,
∴∠NAM=∠NCM,∠BCA=∠NMA,
∵∠BCA=∠NCM,
∴∠NMA=∠NAM,
∴AN=NM.
证明:连接AC、AM,如图.

∵AB=BC,
∴∠BAC=∠BCA,
∴∠BAC=∠BCA=
| 180°-∠ABC |
| 2 |
∵CM平分∠NCD,
∴∠NCM=∠DCM,
∴∠NCM=∠DCM=
| 180°-∠BCD |
| 2 |
∵∠ANM=∠ABC=∠BCD,
∴∠BAC=∠BCA=∠NCM=∠DCM,
∴∠ACM=∠ACD+∠DCM=∠ACD+∠BCA=∠BCD=∠ANM,
∴A、C、N、M四点共圆,
∴∠NAM=∠NCM,∠BCA=∠NMA,
∵∠BCA=∠NCM,
∴∠NMA=∠NAM,
∴AN=NM.
点评:本题考查了四点共圆的判定、等腰三角形的判定与性质、三角形的内角和定理、圆周角定理、圆内接四边形的性质、角平分线的性质等知识,证到∠ACM=∠BCD=∠ANM,进而得到A、C、N、M四点共圆是解决本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
-|-
|的倒数是( )
| 2 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
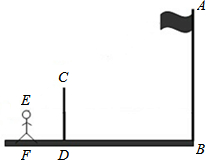 如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆AB的高度.
如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆AB的高度.