题目内容
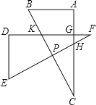
【题目】如图，在
中，
，
，
，以斜边
上距离
点
的点
为中心，把这个三角形按逆时针方向旋转
至
，则旋转前后两个三角形重叠部分的面积是________
．
【答案】
【解析】
过P作PM⊥AC于M，PN⊥DF于N，由以斜边BC上距离B点6cm的点P为中心，把这个三角形按逆时针方向旋转90°至△DEF，根据旋转的性质得∠KPH=90°，∠KGH=90°，得∠MPN=90°，易证Rt△PCM≌Rt△PFN，得到PM=PN，则四边形PMGN为正方形，Rt△PNK≌Rt△PMH，由PM∥AB，PM：AB=CP：CB，得到
，于是
．
过P作PM⊥AC于M，PN⊥DF于N．如图，∵以斜边BC上距离B点6cm的点P为中心，把这个三角形按逆时针方向旋转90°至△DEF，∴∠KPH=90°，∠KGH=90°，∴∠MPN=90°，∴∠KPN=∠MPH．
∵PC=PF，∠C=∠F，∴Rt△PCM≌Rt△PFN，∴PM=PN，∴四边形PMGN为正方形，Rt△PNK≌Rt△PMH，∴S重叠部分=S正方形PMGN．
∵∠A=90°，AB=6，AC=8，∴BC=10，而PB=6，则PC=4．
又∵PM∥AB，∴PM：AB=CP：CB，∴，∴（cm2）．
故答案为：．
练习册系列答案
春雨教育同步作文系列答案
相关题目
