题目内容
 如图所示,O为直线AB上一点,∠BOC=50°,OD平分∠BOC,∠DOE=90°.
如图所示,O为直线AB上一点,∠BOC=50°,OD平分∠BOC,∠DOE=90°.(1)求∠AOE的度数;
(2)OE是否平分∠AOC?请说明理由.
分析:(1)先根据角平分线的定义得出∠DOC=25°,再由余角的性质得出∠COE=65°,然后根据平角的定义即可求出∠AOE的度数;
(2)根据∠COE与∠AOE度数相等即可说明OE平分∠AOC.
(2)根据∠COE与∠AOE度数相等即可说明OE平分∠AOC.
解答:解:(1)∵∠BOC=50°,OD平分∠BOC,
∴∠DOC=
∠BOC=25°,
∵∠DOE=90°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°,
∴∠AOE=180°-∠BOC-∠COE=65°;
(2)OE平分∠BOC.理由如下:
∵∠COE=65°,∠AOE=65°,
∴∠COE=∠AOE,
所以OE平分∠AOC.
∴∠DOC=
| 1 |
| 2 |
∵∠DOE=90°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°,
∴∠AOE=180°-∠BOC-∠COE=65°;
(2)OE平分∠BOC.理由如下:
∵∠COE=65°,∠AOE=65°,
∴∠COE=∠AOE,
所以OE平分∠AOC.
点评:本题主要考查了角的度数的计算,正确理解角平分线的定义,余角的性质以及平角的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,O为直线AB上一点,OM平分∠AOC,ON平分∠BOC,则图中互余的角有( )
如图所示,O为直线AB上一点,OM平分∠AOC,ON平分∠BOC,则图中互余的角有( )| A、1对 | B、2对 | C、3对 | D、4对 |
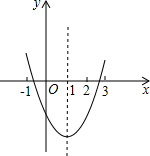 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,则下列结论: 12、二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=2,若与x轴交点为A(6,0),则由图象可知,当y>0时,自变量x的取值范围是
12、二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=2,若与x轴交点为A(6,0),则由图象可知,当y>0时,自变量x的取值范围是 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )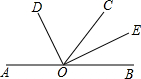 如图所示,O为直线AB上一点,过O点作射线OC.已知OD平分∠AOC、OE平分∠BOC,请问OD与OE有什么位置关系?并说明理由.
如图所示,O为直线AB上一点,过O点作射线OC.已知OD平分∠AOC、OE平分∠BOC,请问OD与OE有什么位置关系?并说明理由.