题目内容
 如图,直线y=kx+b与双曲线
如图,直线y=kx+b与双曲线 交于A(2,1),B(-1,-2)两点,根据图象可得关于x的不等式
交于A(2,1),B(-1,-2)两点,根据图象可得关于x的不等式 的解是________.
的解是________.
0<x<2或x<-1
分析:根据A,B两点的坐标,再根据函数图象的增减性,即可得到不等式 >kx+b的解集.
>kx+b的解集.
解答:函数y=kx+b的图象与函数y=mx的图象交于A,B两点,这两点的横坐标分别是2和-1,
根据图象得到不等式 的解集为0<x<2或x<-1.
的解集为0<x<2或x<-1.
故本题答案为:0<x<2或x<-1.
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.
分析:根据A,B两点的坐标,再根据函数图象的增减性,即可得到不等式
 >kx+b的解集.
>kx+b的解集.解答:函数y=kx+b的图象与函数y=mx的图象交于A,B两点,这两点的横坐标分别是2和-1,
根据图象得到不等式
 的解集为0<x<2或x<-1.
的解集为0<x<2或x<-1.故本题答案为:0<x<2或x<-1.
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
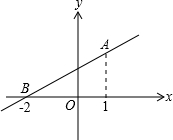 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为