题目内容
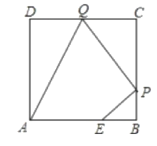
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是___.
【答案】![]()
【解析】
根据最短路径的求法,先确定点E关于BC的对称点E′,再确定点A关于DC的对称点A′,连接A′E′即可得出P,Q的位置;再根据相似得出相应的线段长从而可求得四边形AEPQ的面积.
如图所示:
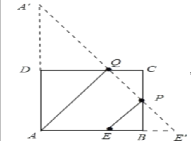
作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ的周长最小,
∵AD=A′D=3,BE=BE′=1,
∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,
∴DQ是△AA′E′的中位线,
∴DQ=![]() AE′=2;CQ=DCCQ=32=1,
AE′=2;CQ=DCCQ=32=1,
∵BP∥AA′,
∴△BE′P∽△AE′A′,
∴![]() ,
,
即![]() ,
,
解得:BP=1.5,
∴CP=BCBP=31.5=1.5,
S四边形AEPQ=S正方形ABCDS△ADQS△PCQS△BEP=9![]() ADDQ
ADDQ![]() CQCP
CQCP![]() BEBP=
BEBP=
=9![]() ×3×2
×3×2![]() ×1×
×1×![]()
![]() ×1×
×1×![]() =
=![]() ,
,
故答案为:![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某公司在A,B两地分别有同型号的机器17台和15台,目前需要把这些机器中的18台运往甲地,14台运往乙地.从A,B两地运往甲,乙两地的费用如表:
甲地(元/台) | 乙地(元/台) | |
A地 | 600 | 500 |
B地 | 400 | 800 |
(1)设从A地运往甲地x台,则从A地运往乙地 台,从B地运往乙地 台.(结果用x的代数式表示,且代数式化到最简)
(2)当运送总费用为15800元时,请确定运送方案(即A,B两地运往甲、乙两地的机器各几台).
(3)能否有一种运送方案比(2)中方案的总运费低?如果有,直接写出运送方案及所需运费;如果没有,请说明理由.
【题目】某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定,现从两家提供的样品中各抽取了6件进行检查,超过标准质量部分记为正数,不足部分记为负数,若该皮具的标准质量为500克,测得它们质量如下(单位:g)
厂家 | 超过标准质量的部分 | |||||
甲 | ﹣3 | 0 | 0 | 1 | 2 | 0 |
乙 | ﹣2 | 1 | ﹣1 | 0 | 1 | 1 |
(1)分别计算甲、乙两厂抽样检测的皮具总质量各是多少克?
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?