题目内容
已知,Rt△ABC的内切圆半径为3,外接圆直径为25,两直角边分别为a、b.则a+b=
- A.36
- B.31
- C.28
- D.24
B
分析:连接OD,OE,根据三角形的内切圆和直角三角形推出四边形ODCE是正方形,得到OD=OE=CD=CE=3,根据直角三角形的外接圆的直径等于直角三角形的斜边长,即推出AB=25,b-3+a-3=AB=25,求出即可.
解答: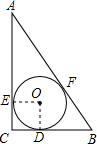 解:连接OD,OE,
解:连接OD,OE,
∵圆O是△ABC的内切圆,
∴AE=AF,BF=BD,∠OEC=∠ODC=∠C=90°,OD=OE,
∴四边形ODCE是正方形,
∵Rt△ABC的内切圆半径为3,
∴OD=OE=CD=CE=3,
∵Rt△ABC的内切圆半径为3,外接圆直径为25,
∴AB=25,b-3+a-3=AB=25,
∴a+b=31.
故选B.
点评:本题主要考查对直角三角形的外接圆和外心,直角三角形的内切圆和内心,正方形的性质和判定,切线长定理等知识点的理解和掌握,此题是一个综合性比较强的题目,题型较好,难度适中.
分析:连接OD,OE,根据三角形的内切圆和直角三角形推出四边形ODCE是正方形,得到OD=OE=CD=CE=3,根据直角三角形的外接圆的直径等于直角三角形的斜边长,即推出AB=25,b-3+a-3=AB=25,求出即可.
解答:
 解:连接OD,OE,
解:连接OD,OE,∵圆O是△ABC的内切圆,
∴AE=AF,BF=BD,∠OEC=∠ODC=∠C=90°,OD=OE,
∴四边形ODCE是正方形,
∵Rt△ABC的内切圆半径为3,
∴OD=OE=CD=CE=3,
∵Rt△ABC的内切圆半径为3,外接圆直径为25,
∴AB=25,b-3+a-3=AB=25,
∴a+b=31.
故选B.
点评:本题主要考查对直角三角形的外接圆和外心,直角三角形的内切圆和内心,正方形的性质和判定,切线长定理等知识点的理解和掌握,此题是一个综合性比较强的题目,题型较好,难度适中.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
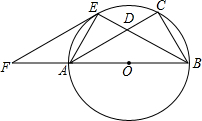 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.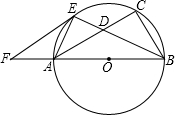 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.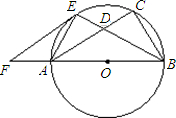 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
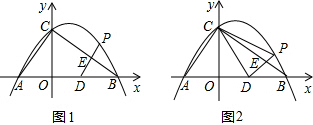 已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).
已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).