Question

如图，一次函数y=2kx+b与反比例函数y=

m

x

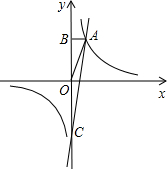相交于第一象限的点A（a，4a），过点A作AB⊥y轴，垂足为B．已知S_△AOB=6．
（1）求反比例函数的关系式及点A的坐标．
（2）若一次函数y=2kx+b与y轴交于点C，S_△AOB与S_△AOC相等，求一次函数的关系式．

Answer 1

分析：（1）由S_△AOB=6可得反比例函数的系数m的值，又A点在反比例函数图象上，可求得a的值，求得A点坐标．
（2）由于S_△AOB与S_△AOC相等可求得C点坐标，再由A、C两点坐标即可确定一次函数的关系式．

解答：解：（1）∵点A（a，4a），AB⊥OB，
∴S_△AOB=

1

2

|a|•|4a|=6．
∴a²=3，a=±

3

．
∵点A在第一象限且在y=

m

x

的图象上，
∴a=

3

，m=12．
即反比例函数关系式为y=

12

x

，点A的坐标为(

3

，4

3

)；

（2）对于函数y=2kx+b，当x=0时，y=b，
∴C（0，b）．
∵S_△AOC=

1

2

OC•AB=

1

2

•|b|•

3

=

3

2

|b|=S_△AOB=6．
∴b=±4

3

．
又∵点A(

3

，4

3

)在y=2kx+b的图象上，
∴当b=4

3

，k=0，此时y=4

3

不是一次函数，
∴k=0舍去．
当b=-4

3

，4

3

=2

3

k-4

3

，
∴k=4．
∴所求一次函数为：y=8x-4

3

．

点评：本题考查了一次函数和反比例函数的综合应用，注意第二问S_△AOB与S_△AOC相等是解题的关键．