题目内容
10.已知$\frac{a+2b-3c}{2}$=$\frac{b-2c+3a}{3}$=$\frac{c+3a+2b}{4}$,则$\frac{a+b+c}{a-b+c}$的值为9.分析 设已知等式等于k,列出方程组,求出方程组的解表示出x,y,z,代入原式计算即可得到结果.
解答 解:设$\frac{a+2b-3c}{2}$=$\frac{b-2c+3a}{3}$=$\frac{c+3a+2b}{4}$=k,
可得$\left\{\begin{array}{l}{a+2b-3c=2k①}\\{b-2c+3a=3k②}\\{c+3a+2b=4k③}\end{array}\right.$,
①×3-②得:5b-7c=3k④,
③-②得:b+3c=k⑤,
④×3+⑤×7得:22b=16k,即b=$\frac{8}{11}$k;
把b=$\frac{8}{11}$k代入⑤得:c=$\frac{1}{11}$k,
把b=$\frac{8}{11}$k,c=$\frac{1}{11}$k代入①得:a=$\frac{9}{11}$k,
则原式=$\frac{\frac{9}{11}+\frac{8}{11}+\frac{1}{11}}{\frac{9}{11}-\frac{8}{11}+\frac{1}{11}}$=9,
故答案为:9
点评 此题考查了解三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
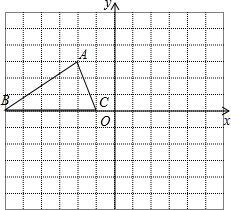 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0). 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径.(精确到0.1m)
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径.(精确到0.1m)