题目内容
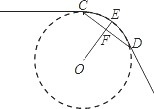
如图,已知⊙O的半径为
,AB=6,△ABC内接于⊙O,BD⊥AC于D,则sin∠CBD的值等于( )

| 10 |
A.
| B.
| C.
| D.3 |

连接OA、OB;
∵OM⊥AB,
∴AM=BM=3,∠AOM=∠BOM=
∠AOB;
又∵∠BCD=
∠AOB,
∴∠BOM=∠BCD,∠OBM=∠CBD;
在Rt△OBM中,
∵OB=
,BM=3,
∴OM=
=
=1,
∴sin∠OBM=sin∠CBD=
=
=
.
故选B.

∵OM⊥AB,
∴AM=BM=3,∠AOM=∠BOM=
| 1 |
| 2 |
又∵∠BCD=
| 1 |
| 2 |
∴∠BOM=∠BCD,∠OBM=∠CBD;
在Rt△OBM中,
∵OB=
| 10 |
∴OM=
| OB2-BM2 |
| 10-9 |
∴sin∠OBM=sin∠CBD=
| OM |
| OB |
| 1 | ||
|
| ||
| 10 |
故选B.


练习册系列答案
相关题目