题目内容
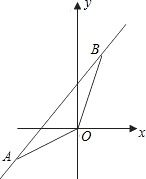
如图,已知一次函数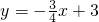 的图象与x轴,y轴分别相交于A,B两点,点C在AB上以
的图象与x轴,y轴分别相交于A,B两点,点C在AB上以 每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.
每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.
(1)求AB的长;
(2)当t为何值时,△ACD与△ABO相似?并直接写出此时点C的坐标.
解:(1)当x=0时,y=3;当y=0时,x=4,
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB= =5;
=5;
(2)依题意BC=t,AC=5-t,AD=t,
若△ACD∽△ABO相似,
∴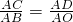 ,
,
代入得:
 ,
,
解得:t= ,
,
∴点C的横坐标也就是AO-AD=AO-t=4- =
= ,
,
再把x= 带入一次函数解析式,得y=
带入一次函数解析式,得y= .
.
∴此时C( ,
, )
)
若△ACD∽△AOB相似,
 ,
,
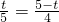 ,
,
∴t= ,
,
AC=5-t= ,
,
再过C点做CE⊥OA于E,
然后△ACE∽ABO,
 =
= ,
,
即 =
= ,
,
解得AE= ,
,
∴OE=AO-AE=4- =
= ,
,
而且又∵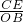 =
= ,即
,即 =
= .
.
解得CE= .所以C(
.所以C( ,
, )
)
∴C( ,
, )或(
)或( ,
, )
)
分析:(1)首先容易求出A,B两点的坐标,然后求出OA,OB的长度,再利用勾股定理求AB;
(2)先用t分别表示AC,AD的长度,再根据相似的性质可以列出关于t的方程,解方程就可以求出点C的坐标;
点评:此题主要考查了一次函数的综合知识,另外还考查了勾股定理的计算及相似三角形的性质.题目难度适中.
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=
 =5;
=5;(2)依题意BC=t,AC=5-t,AD=t,
若△ACD∽△ABO相似,

∴
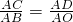 ,
,代入得:
 ,
,解得:t=
 ,
,∴点C的横坐标也就是AO-AD=AO-t=4-
 =
= ,
,再把x=
 带入一次函数解析式,得y=
带入一次函数解析式,得y= .
.∴此时C(
 ,
, )
)若△ACD∽△AOB相似,
 ,
,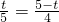 ,
,∴t=
 ,
,AC=5-t=
 ,
,再过C点做CE⊥OA于E,
然后△ACE∽ABO,
 =
= ,
,即
 =
= ,
,解得AE=
 ,
,∴OE=AO-AE=4-
 =
= ,
,而且又∵
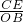 =
= ,即
,即 =
= .
.解得CE=
 .所以C(
.所以C( ,
, )
)∴C(
 ,
, )或(
)或( ,
, )
)分析:(1)首先容易求出A,B两点的坐标,然后求出OA,OB的长度,再利用勾股定理求AB;
(2)先用t分别表示AC,AD的长度,再根据相似的性质可以列出关于t的方程,解方程就可以求出点C的坐标;
点评:此题主要考查了一次函数的综合知识,另外还考查了勾股定理的计算及相似三角形的性质.题目难度适中.

练习册系列答案
相关题目
 如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点.
如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点. 如图,已知一次函数的图象经过点A(-1,0)、B(0,2).
如图,已知一次函数的图象经过点A(-1,0)、B(0,2). 在第一象限,CD⊥x轴于D,若OA=OB=OD=1.
在第一象限,CD⊥x轴于D,若OA=OB=OD=1. 的图象经过
的图象经过 ,
, 两点,并且交x轴于点C,交y轴于点D.
两点,并且交x轴于点C,交y轴于点D.
 的值;
的值; .
. 的图象与
的图象与 轴、
轴、 轴分别交于A、B两点且与反比例函数
轴分别交于A、B两点且与反比例函数 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥ ,A B =
,A B =  ,C D =
,C D = 

