题目内容
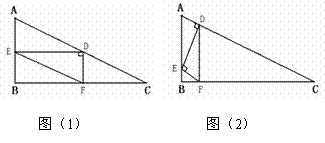
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t 的式子表示AE、AD的长;
(2)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)连接DE,当t为何值时,△DEF为直角三角形?


 (4)如图②,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形
(4)如图②,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形![]() AEA′D为菱形?并判断此时点A是否在BC上?请说明理由.
AEA′D为菱形?并判断此时点A是否在BC上?请说明理由.
![]()
图① 图②
解:(1)AE=t AD=12-2t
(2)∵ DF⊥BC,∠C=30°
∴ DF=![]() CD=
CD=![]() ×2t = t
×2t = t
∵ AE =t
∴ DF= AE
∵ ∠ABC=90°, DF⊥BC
∴ DF∥AE
∴ 四边形AEFD是平行四边形;
(3)①显然 ∠DFE < 90°;
②如图(1),当∠EDF = 90°时,四边形EB![]() FD为矩形,
FD为矩形,
![]() 此时 AE =
此时 AE =![]() AD ∴
AD ∴![]() ∴
∴![]()
③如图(2),当∠DEF = 90°时,此时∠ADE = 90°
![]() ∴∠AED = 90°-∠A=30°
∴∠AED = 90°-∠A=30°
∴AD =![]() AE ∴
AE ∴![]()
∴![]()
综上:当![]() 秒或
秒或![]() 秒时,⊿DEF为直角三角形;
秒时,⊿DEF为直角三角形;
 |
 (4)
(4)
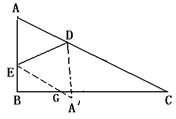
图(3)
如图(3),若四边形AEA′D为菱形,则AE=A![]() D
D
∴t=12-2t
∴t=4
∴当t=4时,四边形AEA′D为菱形
设EA′交BC于点G
在Rt△EBG中,∠BEG=180°-∠AEG=6![]() 0°
0°
∴GE=2BE
∵BE=AB-AE=6-4=2
∴GE=4=EA′
∴点G与点A′重合
∴点A在BC上

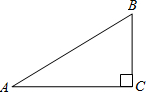 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( )
(2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( ) 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长. 如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC=
如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC= 如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图:
如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图: