题目内容
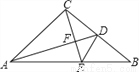
如图,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过点C作AD的垂线,交AB于点F,求证∠ADC=∠BDE
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
题目内容
如图,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过点C作AD的垂线,交AB于点F,求证∠ADC=∠BDE

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案