题目内容
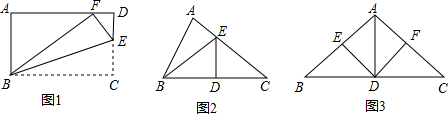
(12分)如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1㎝,设出发的时间为t秒.(1)出发2秒后,求△ABP的周长。
(2)问t为何值时,△BCP是以BC为腰的等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?

(1)当t=2时,CP="2, " 1分

在Rt△BCA中,由勾股定理得
AC="4 "
∴AP="2 " 1分
在Rt△BCP中,由勾股定理得
∴ 1分
1分
∴△ABP的周长=2+5+ =
= 1分
1分
(2)①BC=CP=3cm,有两种情况:
i)若P在边AC上时,
此时t=3s,△BCP为等腰三角形; 1分
ii)若P在AB边上时,CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm, 1分
根据勾股定理可求得BP=3.6cm,
所以P运动的路程为9-3.6=5.4cm,
则用的时间为5.4s,△BCP为等腰三角形 1分
②BP=CB=3cm,
此时AP=2cm,P运动的路程为2+4=6cm, 1分
(3)由题可知P运动的路程为t, Q运动的路程为2t,
要使PQ把△ABC的周长平均分成两份,所以P、Q运动的路程和为6或者比12多6。
∴2t+t=6或2t+t="12+6 " 2分
∴t="2" 或t="6 " 2分解析:
略

在Rt△BCA中,由勾股定理得
AC="4 "
∴AP="2 " 1分
在Rt△BCP中,由勾股定理得
∴
 1分
1分 ∴△ABP的周长=2+5+
 =
= 1分
1分(2)①BC=CP=3cm,有两种情况:
i)若P在边AC上时,
此时t=3s,△BCP为等腰三角形; 1分
ii)若P在AB边上时,CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm, 1分
根据勾股定理可求得BP=3.6cm,
所以P运动的路程为9-3.6=5.4cm,
则用的时间为5.4s,△BCP为等腰三角形 1分
②BP=CB=3cm,
此时AP=2cm,P运动的路程为2+4=6cm, 1分
(3)由题可知P运动的路程为t, Q运动的路程为2t,
要使PQ把△ABC的周长平均分成两份,所以P、Q运动的路程和为6或者比12多6。
∴2t+t=6或2t+t="12+6 " 2分
∴t="2" 或t="6 " 2分解析:
略

练习册系列答案
相关题目
 ,求此时直线PM的解析式;
,求此时直线PM的解析式; ,PM的延长线与CD的延长线交于点F,若三角形G
,PM的延长线与CD的延长线交于点F,若三角形G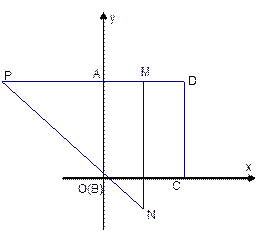
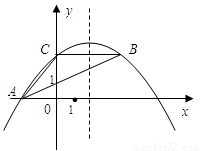
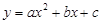 的图象与x轴交于两个不同的点A(-2,0)、B(4,0),与y轴交于点C(0,3),连结BC、AC,该二次函数图象的对称轴与x轴相交于点D.
的图象与x轴交于两个不同的点A(-2,0)、B(4,0),与y轴交于点C(0,3),连结BC、AC,该二次函数图象的对称轴与x轴相交于点D.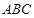 相似,求出点Q的坐标;
相似,求出点Q的坐标;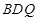 外接圆圆心的坐标.
外接圆圆心的坐标.
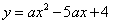 经过
经过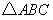 的三个顶点,已知
的三个顶点,已知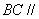
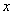 轴,点
轴,点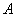 在
在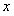 轴上,点
轴上,点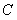 在
在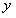 轴上,且
轴上,且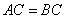 .
.
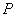 是抛物线对称轴上且在
是抛物线对称轴上且在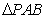 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点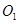 和⊙
和⊙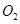 相交于A、B两点,⊙
相交于A、B两点,⊙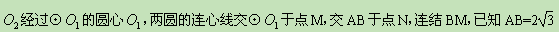
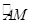 的长。
的长。