题目内容
 如图所示,为求出河对岸两棵树A、B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线前进了12米到达点D,测得∠CDB=90°,取CD的中点E,测得∠AEC=55°,∠BED=66°,求河对岸两棵树间的距离.(结果精确到1米)
如图所示,为求出河对岸两棵树A、B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线前进了12米到达点D,测得∠CDB=90°,取CD的中点E,测得∠AEC=55°,∠BED=66°,求河对岸两棵树间的距离.(结果精确到1米)(参考数据:cos55°=0.576,tan55°=1.43,cos66°=0.407,tan66°=2.25)
分析:根据E为CD中点,CD=12,得到CE=DE=6.在Rt△ACE中,求得AC=CE•tan55°,在Rt△BDE中,求得BD=DE•tan66°,然后利用勾股定理求得AB的长即可.
解答: 解:∵E为CD中点,CD=12m,
解:∵E为CD中点,CD=12m,
∴CE=DE=6m.
在Rt△ACE中,
∵tan55°=
,
∴AC=CE•tan55°=6×1.43=8.58m
在Rt△BDE中,
∵tan66°=
,
∴BD=DE•tan66°=6×2.25=13.5m.
∵AF⊥BD,
∴AC=DF=8.58m,AF=CD=12m,
∴BF=BD-DF=13.5-8.58=4.92m.
在Rt△AFB中,AF=12m,BF=4.92m,
∴AB=
≈13m.
∴河对岸两棵树间的距离约为13米.
 解:∵E为CD中点,CD=12m,
解:∵E为CD中点,CD=12m,∴CE=DE=6m.
在Rt△ACE中,
∵tan55°=
| AC |
| CE |
∴AC=CE•tan55°=6×1.43=8.58m
在Rt△BDE中,
∵tan66°=
| BD |
| DE |
∴BD=DE•tan66°=6×2.25=13.5m.
∵AF⊥BD,
∴AC=DF=8.58m,AF=CD=12m,
∴BF=BD-DF=13.5-8.58=4.92m.
在Rt△AFB中,AF=12m,BF=4.92m,
∴AB=
| AF2+BF2 |
∴河对岸两棵树间的距离约为13米.
点评:本题考查了解直角三角形的应用,解决本题的关键是正确的构造直角三角形,并选择正确的边角关系.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F)
如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F) 如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F)
如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F) ,tan56°≈
,tan56°≈ ,sin67°≈
,sin67°≈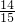 ,tan67°≈
,tan67°≈ )
) ,tan56°≈
,tan56°≈ ,sin67°≈
,sin67°≈ ,tan67°≈
,tan67°≈ )
)
