题目内容
如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=900。取CD的中点E,测∠AEC=560,
∠BED=670,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F)
(参考数据sin560≈![]() ,tan560 ≈
,tan560 ≈![]() ,sin670≈
,sin670≈![]() ,tan670≈
,tan670≈![]() )
)

解:∵E为CD中点,CD=12,
 ∴CE=DE=6.
∴CE=DE=6.
在Rt⊿ACE中,
∵tan56°=![]()
∴AC=CE. tan56°≈6×![]() =9
=9
在Rt△BDE中,∵tan67°= ![]() ,
,
∴BD=DE. tan67°=6×![]() =14 .
=14 .
∵AF⊥BD ,
∴AC=DF=9,AF=CD=12,
∴BF=BD-DF=14-9=5.
在Rt⊿AFB中,AF=12,BF=5,
∴![]()
∴两树间距离为13米。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F)
如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F) 如图所示,为求出河对岸两棵树A、B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线前进了12米到达点D,测得∠CDB=90°,取CD的中点E,测得∠AEC=55°,∠BED=66°,求河对岸两棵树间的距离.(结果精确到1米)
如图所示,为求出河对岸两棵树A、B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线前进了12米到达点D,测得∠CDB=90°,取CD的中点E,测得∠AEC=55°,∠BED=66°,求河对岸两棵树间的距离.(结果精确到1米) 如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F)
如图所示,为求出河对岸两棵树A.B间的距离,小坤在河岸上选取一点C,然后沿垂直于AC的直线的前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°,求河对岸两树间的距离(提示:过点A作AF⊥BD于点F) ,tan56°≈
,tan56°≈ ,sin67°≈
,sin67°≈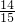 ,tan67°≈
,tan67°≈ )
) ,tan56°≈
,tan56°≈ ,sin67°≈
,sin67°≈ ,tan67°≈
,tan67°≈ )
)