题目内容
如图,在平面直角坐标系中,二次函数 的图象与
的图象与 轴交于A(
轴交于A( ,0),B(2,0),且与
,0),B(2,0),且与 轴交于点C.
轴交于点C.


(1)求该抛物线的解析式,并判断△ABC的形状;
(2)点P是x轴下方的抛物线上一动点, 连接PO,PC,
并把△POC沿CO翻折,得到四边形 ,求出使四边形
,求出使四边形 为菱形的点P的坐标;
为菱形的点P的坐标;
(3) 在此抛物线上是否存在点Q,使得以A,C,B,Q四点为顶点的四边形是直角梯形?若存在, 求出Q点的坐标;若不存在,说明理由.
 的图象与
的图象与 轴交于A(
轴交于A( ,0),B(2,0),且与
,0),B(2,0),且与 轴交于点C.
轴交于点C.

(1)求该抛物线的解析式,并判断△ABC的形状;
(2)点P是x轴下方的抛物线上一动点, 连接PO,PC,
并把△POC沿CO翻折,得到四边形
 ,求出使四边形
,求出使四边形 为菱形的点P的坐标;
为菱形的点P的坐标;(3) 在此抛物线上是否存在点Q,使得以A,C,B,Q四点为顶点的四边形是直角梯形?若存在, 求出Q点的坐标;若不存在,说明理由.

(1)抛物线的解析式为
 ,△ABC是直角三角形
,△ABC是直角三角形
(2)P点的坐标为( ,
, ) 或(
) 或( ,
, )
)
(3)存在,满足题目条件的点Q为( ,
, )或(-
)或(- ,9)
,9)

 ,△ABC是直角三角形
,△ABC是直角三角形 (2)P点的坐标为(
 ,
, ) 或(
) 或( ,
, )
) (3)存在,满足题目条件的点Q为(
 ,
, )或(-
)或(- ,9)
,9)试题分析:(1) 根据题意,将A(
 ,0),B(2,0)代入
,0),B(2,0)代入 中,解得
中,解得抛物线的解析式为




当
 =0时,
=0时, . ∴点C的坐标为(-1,0).
. ∴点C的坐标为(-1,0).∴在△AOC中,AC=
 =
= =
= 。
。在△BOC中,BC=
 =
= =
= 。
。 AB=OA+OB=
 +2=
+2= ,∵AC 2+BC 2=
,∵AC 2+BC 2= +5=
+5= ="AB" 2,
="AB" 2, ∴△ABC是直角三角形。
(2) 设P点坐标为(x,
 ),
), 交CO于E
交CO于E∵四边形POPC是菱形,∴PC=PO.
连结
 则PE⊥CO于E,∴OE=EC=
则PE⊥CO于E,∴OE=EC= ∴
∴ =
= .
.∴
 =
= 解得
解得 =
= ,
, =
=
∴P点的坐标为(
 ,
, ) 或(
) 或( ,
, )
) (3)存在。由(1)知,AC^BC,设Q点坐标为(
 ,
, )
)①若以BC为底边,则BC//AQ,∴∠ABC=∠QAB 如图①
过点Q作QE⊥x轴于点E,则有△QAE∽△ABC ∴

∴
 解得
解得 1=
1=
 2= -
2= - (舍去)。
(舍去)。当
 =
= 时,y=
时,y=  ,∴点Q(
,∴点Q( ,
, )。
)。 k若以AC为底边,则BQ//AC,∴∠CAB=∠QBA
过点Q作QF⊥x轴于点F,则有△QBF∽△BAC ∴

∴
 解得
解得 1=
1=
 2=" 2" (舍去)。
2=" 2" (舍去)。当
 =
= 时,y=9,∴点Q(
时,y=9,∴点Q( ,9)。
,9)。 综上所述,满足题目条件的点Q为(
 ,
, )或(-
)或(- ,9)。
,9)。 点评:本题考查抛物线,勾股定理逆定理,相似三角形,解答本题需要考生掌握待定系数法,会用待定系数法求抛物线的解析式,熟悉勾股定理逆定理,会用其来判定一个三角形是否是直角三角形,掌握相似三角形的方法,会证明两个三角形相似

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目

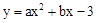 (a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
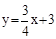 的图象与y轴的交点,点B在二次函数
的图象与y轴的交点,点B在二次函数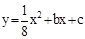 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.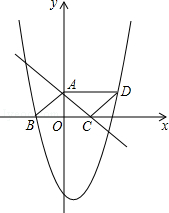
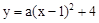 与x轴交于点A,B,与
与x轴交于点A,B,与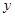 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。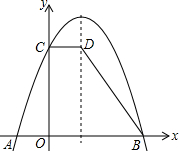
 的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
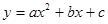 经过点A(-1,0)、B(3,0)、C(0,
经过点A(-1,0)、B(3,0)、C(0,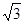 ),连接AC、BC,将△ABC绕点C逆时针旋转,使点A落在x轴上,得到△DCE,此时,DE所在直线与抛物线交于第一象限的点F.
),连接AC、BC,将△ABC绕点C逆时针旋转,使点A落在x轴上,得到△DCE,此时,DE所在直线与抛物线交于第一象限的点F.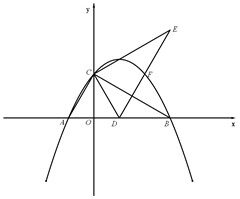
 (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是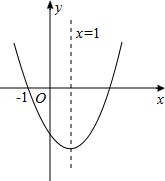
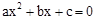 (a≠0)的一个根
(a≠0)的一个根