题目内容
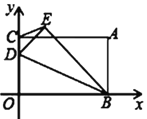
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与直线
,与直线![]() 交于点
交于点![]() 和点
和点![]() ,
,![]() 为抛物线的顶点,直线
为抛物线的顶点,直线![]() 是抛物线的对称轴.
是抛物线的对称轴.
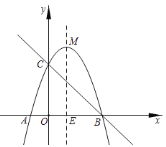
(1)求抛物线的解析式及点![]() 的坐标.
的坐标.
(2)点![]() 为直线
为直线![]() 上方抛物线上一点,设
上方抛物线上一点,设![]() 为点
为点![]() 到直线
到直线![]() 的距离,当
的距离,当![]() 有最大值时,求点
有最大值时,求点![]() 的坐标.
的坐标.
(3)若点![]() 为直线
为直线![]() 上一点,作点
上一点,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是直角三角形时,直接写出点
是直角三角形时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先由直线解析式求出B点坐标,再把A,B坐标代入抛物线解析式中,求出a,c的值,从而求出抛物线解析式,再把抛物线解析式化成顶点式,求出顶点坐标即可;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,写出△PCB面积的表达式,求出△PCB面积最大值所对应的m,从而求出P点坐标;
,写出△PCB面积的表达式,求出△PCB面积最大值所对应的m,从而求出P点坐标;
(3)由题意,知![]() ,
,![]() .设点
.设点![]() 的坐标为
的坐标为![]() ,分别求出
,分别求出![]() ,
,![]() ,
,![]() ,在分类讨论①当
,在分类讨论①当![]() 时,
时,![]() ,②当
,②当![]() 时,
时,![]() ,求出t,即可求出F的坐标.
,求出t,即可求出F的坐标.
解:(1)∵直线![]() ,
,
令y=0,解得x=3,
∴![]() ,
,
将点![]() ,
,![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]() ,解得
,解得![]()
∴抛物线的解析式为![]() ,
,
∵![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,如解图所示,
,如解图所示,
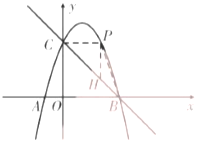
由题意,可知![]() 有最大值时,
有最大值时,![]() 有最大值,
有最大值,
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 有最大值,且最大值为
有最大值,且最大值为![]() ,此时
,此时![]() 有最大值,
有最大值,
∴点![]() 的坐标为
的坐标为![]() ;
;
(3)由题意,知![]() ,
,![]() .设点
.设点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
由题,易知![]() ,则当
,则当![]() 是直角三角形时,需分以下两种情况进行讨论,
是直角三角形时,需分以下两种情况进行讨论,
①当![]() 时,
时,![]() ,
,
即![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
②当![]() 时,
时,![]() ,
,
即![]() ,解得
,解得![]() (与点
(与点![]() 重合,故舍去)或
重合,故舍去)或![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

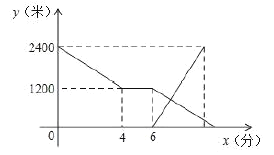
【题目】某书店店主对书店销售情况进行统计,店主根据一个月内平均每天各销售时间段内的销售量,绘制了如下尚不完整的统计图表.
销售情况扇形统计图
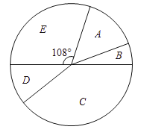
销售情况统计表
销售时间段 | 销售数量(本) |
| 16 |
|
|
| 37 |
| 12 |
| 30 |
合计 |
|
根据以上信息,回答下列问题:
(1)平均每天的销售总量![]() ________,
________,![]() 时间段每天的销售数量
时间段每天的销售数量![]() ___________.
___________.
(2)求出![]() 时间段所在扇形的圆心角的度数.
时间段所在扇形的圆心角的度数.
(3)若该书店一年的销量有32000本,请你估计![]() 时间段全年卖出多少本.
时间段全年卖出多少本.
(4)若书店决定减少成本,同时保证销量,决定在某时间段闭店,请你提出一条合理化的建议.
【题目】某汽车经销商为了能更好的了解某季度纯电动汽车的续航能力,现分两次不重复的各抽取了10台纯电动车进行了续航里程的测试.并将测试的情况进行整理、描述和分析(续航里程用x表示,共分成四组:(A)100≤x<200,(B)200≤x<300,(C)300≤x<400,(D)x≥400,单位:km).下面给出了部分信息:
第一次抽取10台车的续航里程在C组中的数据是:380,310,300,310.
第二次抽取10台车的续航里程是:220,301,175,310,400,310,385,430,234,455.
第一次测试的续航里程扇形统计图如图
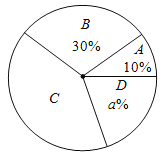
两次测试的续航里程统计表
第一次 | 第二次 | |
平均里程 | 321.4 | b |
中位数 | c | 310 |
众数 | 310 | 310 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中a、b、c的值,a= ,b= ,c .
(2)根据以上数据,你认为这两次测试中的哪一次的纯电动汽车续航能力更强?请说明理由(一条理由即可).
(3)若经销商这一季度共购进1600台纯电动汽车,结合这两次测试,估计这一季度续航能力较强(x≥380)的纯电动汽车有多少辆?