题目内容
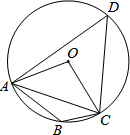 如图,四边形ABCD内接于⊙O,∠ABC=130°,求∠OAC的度数.
如图,四边形ABCD内接于⊙O,∠ABC=130°,求∠OAC的度数.考点:圆内接四边形的性质,圆周角定理
专题:
分析:先根据圆内接四边形的性质推出∠ADC=50°,再根据圆周角定理推出∠AOC=100°,然后根据等腰三角形的性质及三角形内角和定理即可得出∠OAC的度数.
解答:解:∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠ABC=130°,
∴∠ADC=180°-∠ABC=50°,
∴∠AOC=2∠ADC=100°.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=
(180°-∠AOC)=40°.
∴∠ADC+∠ABC=180°,
∵∠ABC=130°,
∴∠ADC=180°-∠ABC=50°,
∴∠AOC=2∠ADC=100°.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=
| 1 |
| 2 |
点评:本题主要考查圆内接四边形的性质、圆周角定理、等腰三角形的性质及三角形内角和定理,关键在于求出∠AOC的度数.

练习册系列答案
相关题目
 有理数a,b在数轴上的位置如图所示.化简|a+b|的结果为( )
有理数a,b在数轴上的位置如图所示.化简|a+b|的结果为( )| A、a-b | B、a+b |
| C、-a+b | D、-a-b |
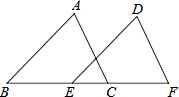 如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=70°,求∠ACB的度数.
如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=70°,求∠ACB的度数.
 如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+3过A,B,C三点且AB=6.
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+3过A,B,C三点且AB=6.