题目内容
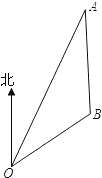
如图，在△ABC中，已知AB=15，BC=14，S△ABC=84．求：（1）tanC的值；（2）sinA的值．
（1）过A作AD⊥BC于点D．
∵S△ABC=
BC•AD=84，∴
×14×AD=84，∴AD=12．
又∵AB=15，∴BD=
=
=9．
∴CD=14-9=5．
在Rt△ADC中，AC=
=
=13，
∴tanC=
=
（2）过B作BE⊥AC于点E．
∵S△ABC=
AC•EB=84，
∴BE=
，
∴sin∠BAC=
=
=
=
．
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB=15，∴BD=
| AB2-AD2 |
| 152-122 |
∴CD=14-9=5．
在Rt△ADC中，AC=
| AD2+DC2 |
| 122+52 |
∴tanC=
| AD |
| DC |
| 12 |
| 5 |
（2）过B作BE⊥AC于点E．
∵S△ABC=
| 1 |
| 2 |
∴BE=
| 168 |
| 13 |
∴sin∠BAC=
| BE |
| AB |
| ||
| 15 |
| 168 |
| 195 |
| 56 |
| 65 |
练习册系列答案
相关题目
