题目内容
【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2 ![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 , 点A的坐标为 , 点B的坐标为;
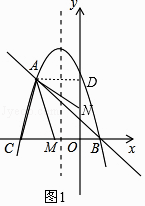
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
【答案】
(1)y=﹣ ![]() x+
x+ ![]() ;(﹣2,2
;(﹣2,2 ![]() );(1,0)
);(1,0)
(2)
解:如图1,过A作AD⊥y轴于点D,
在y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2 ![]() 中,令y=0可求得x=﹣3或x=1,
中,令y=0可求得x=﹣3或x=1,
∴C(﹣3,0),且A(﹣2,2 ![]() ),
),
∴AC= ![]() =
= ![]() ,
,
由翻折的性质可知AN=AC= ![]() ,
,
∵△AMN为梦想三角形,
∴N点在y轴上,且AD=2,
在Rt△AND中,由勾股定理可得DN= ![]() =
= ![]() =3,
=3,
∵OD=2 ![]() ,
,
∴ON=2 ![]() ﹣3或ON=2
﹣3或ON=2 ![]() +3,
+3,
∴N点坐标为(0,2 ![]() ﹣3)或(0,2
﹣3)或(0,2 ![]() +3)
+3)
(3)
解:①当AC为平行四边形的边时,如图2,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,
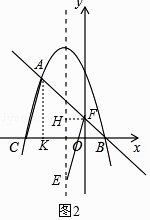
则有AC∥EF且AC=EF,
∴∠ACK=∠EFH,
在△ACK和△EFH中
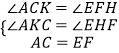
∴△ACK≌△EFH(AAS),
∴FH=CK=1,HE=AK=2 ![]() ,
,
∵抛物线对称轴为x=﹣1,
∴F点的横坐标为0或﹣2,
∵点F在直线AB上,
∴当F点横坐标为0时,则F(0, ![]() ),此时点E在直线AB下方,
),此时点E在直线AB下方,
∴E到y轴的距离为EH﹣OF=2 ![]() ﹣
﹣ ![]() =
= ![]() ,即E点纵坐标为﹣
,即E点纵坐标为﹣ ![]() ,
,
∴E(﹣1,﹣ ![]() );
);
当F点的横坐标为﹣2时,则F与A重合,不合题意,舍去;
②当AC为平行四边形的对角线时,
∵C(﹣3,0),且A(﹣2,2 ![]() ),
),
∴线段AC的中点坐标为(﹣2.5, ![]() ),
),
设E(﹣1,t),F(x,y),
则x﹣1=2×(﹣2.5),y+t=2 ![]() ,
,
∴x=﹣4,y=2 ![]() ﹣t,
﹣t,
代入直线AB解析式可得2 ![]() ﹣t=﹣
﹣t=﹣ ![]() ×(﹣4)+
×(﹣4)+ ![]() ,解得t=﹣
,解得t=﹣ ![]() ,
,
∴E(﹣1,﹣ ![]() ),F(﹣4,
),F(﹣4, ![]() );
);
综上可知存在满足条件的点F,此时E(﹣1,﹣ ![]() )、F(0,
)、F(0, ![]() )或E(﹣1,﹣
)或E(﹣1,﹣ ![]() )、F(﹣4,
)、F(﹣4, ![]() ).
).
【解析】解:(1)∵抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2 ![]() ,
,
∴其梦想直线的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
联立梦想直线与抛物线解析式可得 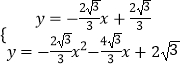 ,解得
,解得 ![]() 或
或 ![]() ,
,
∴A(﹣2,2 ![]() ),B(1,0),
),B(1,0),
【考点精析】掌握平行四边形的判定与性质和翻折变换(折叠问题)是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案