题目内容
把含30°角的三角板ABC，绕点B逆时针旋转90°到三角板DBE位置（如图所示），求sin∠ADE的值．
解：过点E作EF⊥AD，且交AD于点F；设BD=x，则AB=x，BE=
x，AD=
x；在Rt△AEF中，AE=x-
x=
x；易得EF=
•AE=
x；则AF=EF=
x，在Rt△DEF中，
根据三角函数的定义可得：sin∠ADE=
=
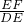；答：sin∠ADE的值为
．分析：过点E作EF⊥AD，且交AD于点F；设BD=x，进而可得AB、BE、AD的值，利用边的关系可得AE的值；在Rt△AEF中，由三角函数的定义可得EF、AF的值；最后在Rt△DEF中，根据三角函数的定义可得sin∠ADE的值．
点评：本题考查锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
把含30°角的三角板ABC，绕点B逆时针旋转90°到三角板DBE位置（如图所示），求sin∠ADE的值．
22、一副直角三角板叠放如图所示，现将含45°角的三角板ADE固定不动，把含30°角的三角板ABC绕顶点A顺时针旋转∠α（α=∠BAD且0°＜α＜180°），使两块三角板至少有一组边平行．
一副直角三角板叠放如图所示，现将含45°角的三角板ADE固定不动，把含30°角的三角板ABC绕顶点A顺时针旋转∠α（α=∠BAD且0°＜α＜180°），使两块三角板至少有一组边平行．则∠α的值有（ ）
