题目内容
如图所示，AB是⊙O的直径，弦AC，BD相交于E，则
等于（ ）
A．tan∠AED
B．cot∠AED
C．sin∠AED
D．cos∠AED
【答案】分析：由圆周角定理得出的相等角，易证得△CDE∽△BAE，则CD：AB=DE：AE；
连接AD，根据圆周角定理可知：∠ADB=90°．
在Rt△ADE中，cos∠AED=
，由此得解．
解答：
解：连接AD，则∠ADB=90°．
∵∠D=∠A，∠C=∠B，（圆周角定理）
∴△CDE∽△BAE．
∴
．
在Rt△ADE中，cos∠AED=
=
．
故选D．
点评：本题主要考查圆周角定理、相似三角形的判定和性质、锐角三角函数的定义等知识．
连接AD，根据圆周角定理可知：∠ADB=90°．
在Rt△ADE中，cos∠AED=
，由此得解．解答：
解：连接AD，则∠ADB=90°．∵∠D=∠A，∠C=∠B，（圆周角定理）
∴△CDE∽△BAE．
∴
．在Rt△ADE中，cos∠AED=
=．故选D．
点评：本题主要考查圆周角定理、相似三角形的判定和性质、锐角三角函数的定义等知识．
练习册系列答案
中考解读考点精练系列答案
相关题目
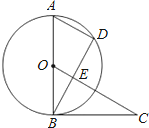如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A．
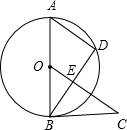如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A，OC⊥BD于点E．
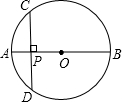如图所示，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，则⊙O的半径为
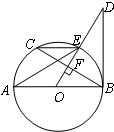如图所示，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，且∠AEC=∠ODB．
如图所示，AB是⊙O直径，∠D=35°，则∠BOC等于（ ）