题目内容
(2012•南宁)已知二次函数y=ax2+bx+1,一次函数y=k(x-1)-
,若它们的图象对于任意的非零实数k都只有一个公共点,则a,b的值分别为( )
| k2 |
| 4 |
分析:根据题意由y=ax2+bx+1①,y=k(x-1)-
②,组成的方程组只有一组解,消去y,整理得,ax2+(b-k)x+1+k+
=0,则△=(b-k)2-4a(1+k+
)=0,整理得到(1-a)k2-2(2a+b)k+b2-4a=0,由于对于任意的实数k都成立,所以有1-a=0,2a+b=0,b2-4a=0,求出a,b即可.
| k2 |
| 4 |
| k2 |
| 4 |
| k2 |
| 4 |
解答:解:根据题意得,
y=ax2+bx+1①,
y=k(x-1)-
②,
解由①②组成的方程组,消去y,整理得,ax2+(b-k)x+1+k+
=0,
∵它们的图象对于任意的实数k都只有一个公共点,则方程组只有一组解,
∴x有两相等的值,
即△=(b-k)2-4a(1+k+
)=0,
∴(1-a)k2-2(2a+b)k+b2-4a=0,
由于对于非零实数k都成立,所以有1-a=0,2a+b=0,
∴b2-4a=0,
∴a=1,b=-2,
故选B.
y=ax2+bx+1①,
y=k(x-1)-
| k2 |
| 4 |
解由①②组成的方程组,消去y,整理得,ax2+(b-k)x+1+k+
| k2 |
| 4 |
∵它们的图象对于任意的实数k都只有一个公共点,则方程组只有一组解,
∴x有两相等的值,
即△=(b-k)2-4a(1+k+
| k2 |
| 4 |
∴(1-a)k2-2(2a+b)k+b2-4a=0,
由于对于非零实数k都成立,所以有1-a=0,2a+b=0,
∴b2-4a=0,
∴a=1,b=-2,
故选B.
点评:本题考查了用待定系数法求抛物线的解析式.二次函数的一般式:y=ax2+bx+c(a≠0);也考查了利用方程组的解的情况确定函数图象交点的问题,而方程组的解的情况转化为一元二次方程根的情况.

练习册系列答案
相关题目
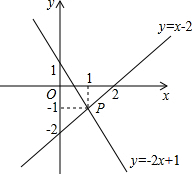 (2012•南宁)如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组
(2012•南宁)如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组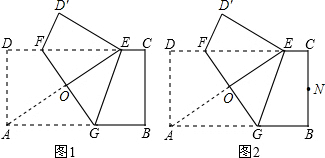 A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.
A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.