题目内容
(2012•南宁)已知点A(3,4),点B为直线x=-1上的动点,设B(-1,y).
(1)如图1,若点C(x,0)且-1<x<3,BC⊥AC,求y与x之间的函数关系式;
(2)在(1)的条件下,y是否有最大值?若有,请求出最大值;若没有,请说明理由;
(3)如图2,当点B的坐标为(-1,1)时,在x轴上另取两点E,F,且EF=1.线段EF在x轴上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标.

(1)如图1,若点C(x,0)且-1<x<3,BC⊥AC,求y与x之间的函数关系式;
(2)在(1)的条件下,y是否有最大值?若有,请求出最大值;若没有,请说明理由;
(3)如图2,当点B的坐标为(-1,1)时,在x轴上另取两点E,F,且EF=1.线段EF在x轴上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标.

分析:(1)过点A作AE⊥x轴于点E,先证明△BCD∽△CAE,再根据相似三角形对应边成比例即可求出y与x之间的函数关系式;
(2)先运用配方法将y=-
x2+
x+
写成顶点式,再根据自变量x的取值范围即可求解;
(3)欲使四边形ABEF的周长最小,由于线段AB与EF是定长,所以只需BE+AF最小.为此,先确定点E、F的位置:过点A作x轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B关于x轴的对称点B′,连接A′B′,交x轴于点E,在x轴上截取线段EF=1,则点E、F的位置确定.再根据待定系数法求出直线A′B′的解析式,然后令y=0,即可求出点E的横坐标,进而得出点E的坐标.
(2)先运用配方法将y=-
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
(3)欲使四边形ABEF的周长最小,由于线段AB与EF是定长,所以只需BE+AF最小.为此,先确定点E、F的位置:过点A作x轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B关于x轴的对称点B′,连接A′B′,交x轴于点E,在x轴上截取线段EF=1,则点E、F的位置确定.再根据待定系数法求出直线A′B′的解析式,然后令y=0,即可求出点E的横坐标,进而得出点E的坐标.
解答: 解:(1)如图1,过点A作AE⊥x轴于点E.
解:(1)如图1,过点A作AE⊥x轴于点E.
在△BCD与△CAE中,
∵∠BCD=∠CAE=90°-∠ACE,∠BDC=∠CEA=90°,
∴△BCD∽△CAE,
∴BD:CE=CD:AE,
∵A(3,4),B(-1,y),C(x,0)且-1<x<3,
∴y:(3-x)=(x+1):4,
∴y=-
x2+
x+
(-1<x<3);
(2)y有最大值.理由如下:
∵y=-
x2+
x+
=-
(x2-2x)+
=-
(x-1)2+1,
又∵-1<x<3,
∴当x=1时,y有最大值1;

(3)如图2,过点A作x轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B关于x轴的对称点B′,连接A′B′,交x轴于点E,在x轴上截取线段EF=1,则此时四边形ABEF的周长最小.
∵A(3,4),∴A′(2,4),
∵B(-1,1),∴B′(-1,-1).
设直线A′B′的解析式为y=kx+b,
则
,
解得
.
∴直线A′B′的解析式为y=
x+
,
当y=0时,
x+
=0,解得x=-
.
故线段EF平移至如图2所示位置时,四边形ABEF的周长最小,此时点E的坐标为(-
,0).
 解:(1)如图1,过点A作AE⊥x轴于点E.
解:(1)如图1,过点A作AE⊥x轴于点E.在△BCD与△CAE中,
∵∠BCD=∠CAE=90°-∠ACE,∠BDC=∠CEA=90°,
∴△BCD∽△CAE,
∴BD:CE=CD:AE,
∵A(3,4),B(-1,y),C(x,0)且-1<x<3,
∴y:(3-x)=(x+1):4,
∴y=-
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
(2)y有最大值.理由如下:
∵y=-
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
又∵-1<x<3,
∴当x=1时,y有最大值1;

(3)如图2,过点A作x轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B关于x轴的对称点B′,连接A′B′,交x轴于点E,在x轴上截取线段EF=1,则此时四边形ABEF的周长最小.
∵A(3,4),∴A′(2,4),
∵B(-1,1),∴B′(-1,-1).
设直线A′B′的解析式为y=kx+b,
则
|
解得
|
∴直线A′B′的解析式为y=
| 5 |
| 3 |
| 2 |
| 3 |
当y=0时,
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
故线段EF平移至如图2所示位置时,四边形ABEF的周长最小,此时点E的坐标为(-
| 2 |
| 5 |
点评:本题考查了相似三角形的性质与判定,待定系数法求一次函数的解析式,轴对称-最短路线问题,综合性较强,有一定难度.(1)中通过作辅助线证明△BCD∽△CAE是解题的关键,(3)中根据“两点之间,线段最短”确定点E、F的位置是关键,也是难点.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
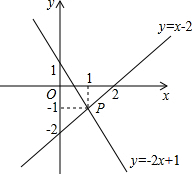 (2012•南宁)如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组
(2012•南宁)如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组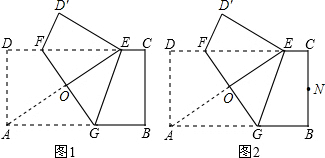 A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.
A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.