Question

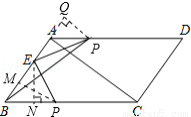
如图，□ABCD中，AC⊥AB ，AB=3cm，BC=5cm，点E为AB上一点，且AE=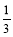AB．点P从B点出发，以1cm/s的速度沿BC→CD→DA运动至A点停止. 则当运动时间为 秒时，△BEP为等腰三角形．

 

 

Answer 1

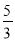，2，，

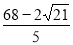
【解析】

试题分析：∵∠BAC=90°，BC=5cm，AB=3cm，′

由勾股定理得：AC=4cm，

即AB、CD间的最短距离是4cm，

∵AB=3cm，AE=AB，

∴AE=1cm，BE=2cm，

设经过ts时，△BEP是等腰三角形，

当P在BC上时，

①BP=EB=2cm，

t=2时，△BEP是等腰三角形；

②BP=PE，

作PM⊥AB于M，

∴BM=ME=BE=1cm

∵cos∠ABC===，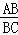

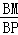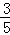∴BP=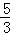cm，

t=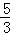时，△BEP是等腰三角形；

③BE=PE=2cm，

作EN⊥BC于N，则BP=2BN，

∴cosB==，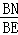

∴=，

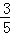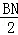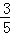BN=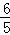cm，

∴BP=，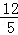

∴t=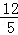时，△BEP是等腰三角形；

当P在CD上不能得出等腰三角形，

∵AB、CD间的最短距离是4cm，CA⊥AB，CA=4cm，

当P在AD上时，只能BE=EP=2cm，

过P作PQ⊥BA于Q，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠QAD=∠ABC，

∵∠BAC=∠Q=90°，

∴△QAP∽△ABC，

∴PQ：AQ：AP=4：3：5，

设PQ=4xcm，AQ=3xcm，

在△EPQ中，由勾股定理得：（3x+1）2+（4x）2=22，

∴x=，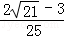

AP=5x=cm，

∴t=5+5+3﹣=，

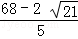答：从运动开始经过2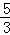s或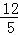s或s或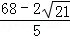s时，△BEP为等腰三角形．

考点: 平行四边形综合题