题目内容
若圆的半径是4cm,一条弦长是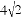 ,则圆心到该弦的距离是_____,该弦所对的圆心角的度数为_____.
,则圆心到该弦的距离是_____,该弦所对的圆心角的度数为_____.
练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
题目内容
若圆的半径是4cm,一条弦长是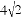 ,则圆心到该弦的距离是_____,该弦所对的圆心角的度数为_____.
,则圆心到该弦的距离是_____,该弦所对的圆心角的度数为_____.
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案