Question

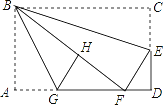
【题目】如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，①∠EBG=45°；②△DEF∽△ABG；③S△ABG=S△FGH；④AG+DF=FG．则下列结论正确的有（ ）

A. ①②④ B. ①③④ C. ②③④ D. ①②③

Answer 1

【答案】B

【解析】

由折叠性质得∠1=∠2，CE=FE，BF=BC=10，则在Rt△ABF中利用勾股定理可计算出AF=8，所以DF=AD-AF=2，设EF=x，则CE=x，DE=CD-CE=6-x，在Rt△DEF中利用勾股定理得（6-x）2+22=x2，解得，即；再利用折叠性质得∠3=∠4，BH=BA=6，AG=HG，易得∠2+∠3=45°，于是可对①进行判断；设AG=y，则GH=y，GF=8-y，在Rt△HGF中利用勾股定理得到y2+42=（8-y）2，解得y=3，则AG=GH=3，GF=5，由于∠A=∠D和，可判断△ABG与△DEF不相似，则可对②进行判断；根据三角形面积公式可对③进行判断；利用AG=3，GF=5，DF=2可对④进行判断．

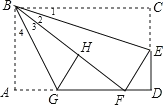
∵△BCE沿BE折叠，点C恰落在边AD上的点F处，
∴∠1=∠2，CE=FE，BF=BC=10，
在Rt△ABF中，∵AB=6，BF=10，
∴，
∴DF=AD-AF=10-8=2，
设EF=x，则CE=x，DE=CD-CE=6-x，
在Rt△DEF中，∵DE2+DF2=EF2，
∴（6-x）2+22=x2，解得，
∴，
∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，
∴∠3=∠4，BH=BA=6，AG=HG，
∴，所以①正确；
HF=BF-BH=10-6=4，
设AG=y，则GH=y，GF=8-y，
在Rt△HGF中，∵GH2+HF2=GF2，
∴y2+42=（8-y）2，解得y=3，
∴AG=GH=3，GF=5，
∵∠A=∠D，

，

，
∴，
∴△ABG与△DEF不相似，所以②错误；
∵，

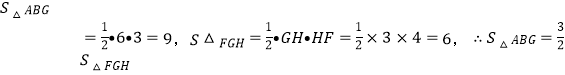所以③正确；
∵AG+DF=3+2=5，而GF=5，
∴AG+DF=GF，所以④正确．
故答案为B．