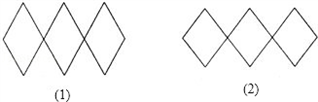
题目内容
如图所示的是我们熟悉的衣帽架,它是由三个菱形组成的,菱形的边长为20cm,当处于图(1)所示的形状时,衣帽架总长为72cm,这时衣帽架的宽度是 拉开,如图(2)所示,使总长度变为96cm,则它的宽度变成
拉开,如图(2)所示,使总长度变为96cm,则它的宽度变成分析:两题的思路一样:根据总长求出一条对角线的长,再根据菱形对角线的性质和勾股定理求得,另一对角线的一半,从而求得另一对角线的长.
解答: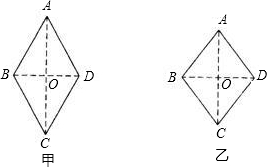 解:(1)由图(1)可以作出如图甲的图形.连接AC,BD,则BD=72÷3=24(cm),
解:(1)由图(1)可以作出如图甲的图形.连接AC,BD,则BD=72÷3=24(cm),
∵四边形ABCD是菱形
∴AC⊥BD,OB=
BD=
×24=12(cm),AC=2OA
∵AB=20cm
∴OA=
=
=16(cm)
∴AC=2×16=32(cm)
∴衣帽架的宽度是32cm
(2)由图(2)可以作出如图乙的图形
连接AC,BD,则BD=96÷3=32(cm)
由(1)中方法可得OA=12cm
∴AC=2×12=24(cm)
∴衣帽架的宽度变成24cm.
 解:(1)由图(1)可以作出如图甲的图形.连接AC,BD,则BD=72÷3=24(cm),
解:(1)由图(1)可以作出如图甲的图形.连接AC,BD,则BD=72÷3=24(cm),∵四边形ABCD是菱形
∴AC⊥BD,OB=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=20cm
∴OA=
| AB2-OB2 |
| 202-122 |
∴AC=2×16=32(cm)
∴衣帽架的宽度是32cm
(2)由图(2)可以作出如图乙的图形
连接AC,BD,则BD=96÷3=32(cm)
由(1)中方法可得OA=12cm
∴AC=2×12=24(cm)
∴衣帽架的宽度变成24cm.
点评:此题主要考查菱形的基本性质:菱形的对角线互相垂直平分,综合利用了勾股定理的内容.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图的图案是一次国际数学教育大会(ICME)的会徽,这个会徽图案中蕴藏着许多我们熟悉的数学知识、会徽的主体图案是由一连串如图所示的直角三角形演化而成的,其中OA1=A1A2=A2A3…=A8A9,那么图中第一个小于30°的锐角是( )
如图的图案是一次国际数学教育大会(ICME)的会徽,这个会徽图案中蕴藏着许多我们熟悉的数学知识、会徽的主体图案是由一连串如图所示的直角三角形演化而成的,其中OA1=A1A2=A2A3…=A8A9,那么图中第一个小于30°的锐角是( )| A、∠A2OA3 | B、∠A3OA4 | C、∠A4OA5 | D、∠A5OA6 |
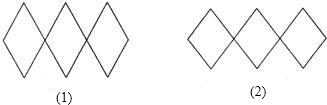 拉开,如图(2)所示,使总长度变为96cm,则它的宽度变成______cm.
拉开,如图(2)所示,使总长度变为96cm,则它的宽度变成______cm.