题目内容
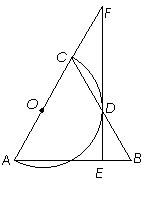
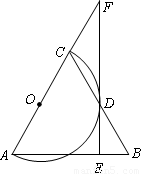
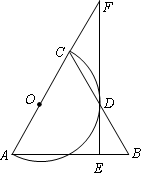
如图,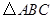 是等腰三角形,
是等腰三角形,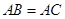 ,以
,以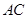 为直径的
为直径的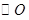 与
与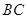 交于点
交于点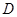 ,
,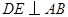 ,垂足为
,垂足为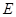 ,
,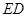 的延长线与
的延长线与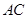 的延长线交于点
的延长线交于点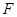 .
.
(1)求证: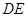 是
是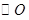 的切线;
的切线;
(2)若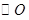 的半径为2,
的半径为2,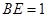 ,求
,求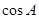 的值.
的值.
【答案】
【解析】
试题分析:(1)连接 、
、 ,先根据圆周角定理可得
,先根据圆周角定理可得 ,由
,由 根据等腰三角形的性质可得
根据等腰三角形的性质可得 是
是 的中点,再结合
的中点,再结合 是
是 的中点,可得
的中点,可得 ,再由
,再由 即可证得结论;
即可证得结论;
(2)由(1)知 ,则有
,则有 ,即得
,即得 ,可解得
,可解得 ,再有
,再有 即可求得结果.
即可求得结果.
(1)连接 、
、 .
.

∵ 是直径
是直径
∴
∵ ,
,
∴ 是
是 的中点.
的中点.
又∵ 是
是 的中点,
的中点,
∴
∵ ,
,
∴ .
.
∴ 是
是 的切线;
的切线;
(2)由(1)知 ,
,
∴
∴ ,
,
∴ .
.
解得 .
.
∴
∴ .
.
考点:圆周角定理,三角形的中位线定理,等腰三角形的性质,切线的判定,平行线等分线段成比例
点评:在证明切线的问题时,一般先连接切点与圆心,再证明垂直即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 8、如图CD是等腰三角形ABC的对称轴,DE⊥CB于E,∠B=55°,则∠CDE的度数是( )
8、如图CD是等腰三角形ABC的对称轴,DE⊥CB于E,∠B=55°,则∠CDE的度数是( ) 正三角形ADE,当△ABC的面积是25
正三角形ADE,当△ABC的面积是25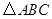 是等腰三角形,
是等腰三角形,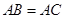 ,以
,以 为直径的
为直径的 与
与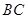 交于点
交于点 ,
, ,垂足为
,垂足为 ,
, 的延长线与
的延长线与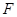 .
.
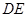 是
是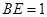 ,求
,求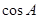 的值.
的值.