题目内容
已知α、β是方程x2-7x+8=0的两个根,且α>β,不解方程,利用根与系数的关系,求 的值.
的值.
解:由题可得:α+β=7,αβ=8,
则α2+β2=(α+β)2-2αβ=33,(α-β)2=(α+β)2-4αβ=17,
而α>β,则α-β= ,
,
设A=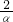 +3β2,B=
+3β2,B=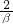 +3α2,
+3α2,
A+B=2( +
+ )+3(α2+β2)=
)+3(α2+β2)=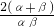 +3(α2+β2)=
+3(α2+β2)=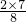 +3×33=100
+3×33=100 ,
,
A-B=2( -
- )+3(β2-α2)=
)+3(β2-α2)=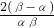 +3(β+α)(β-α)=
+3(β+α)(β-α)=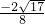 +3×7×(-2
+3×7×(-2 )=-
)=-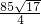 ,
,
∴A= (100
(100 -
-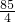
 )=
)= (403-85
(403-85 ),
),
即 =
= (403-85
(403-85 ).
).
分析:由题可得:α+β=7,αβ=8,则α2+β2=(α+β)2-2αβ=33,(α-β)2=(α+β)2-4αβ=17,而α>β,则α-β= ,设A=
,设A=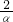 +3β2,B=
+3β2,B=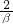 +3,求出A+B及A-B即可得出答案.
+3,求出A+B及A-B即可得出答案.
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
则α2+β2=(α+β)2-2αβ=33,(α-β)2=(α+β)2-4αβ=17,
而α>β,则α-β=
 ,
,设A=
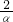 +3β2,B=
+3β2,B=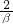 +3α2,
+3α2,A+B=2(
 +
+ )+3(α2+β2)=
)+3(α2+β2)=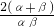 +3(α2+β2)=
+3(α2+β2)=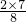 +3×33=100
+3×33=100 ,
,A-B=2(
 -
- )+3(β2-α2)=
)+3(β2-α2)=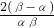 +3(β+α)(β-α)=
+3(β+α)(β-α)=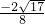 +3×7×(-2
+3×7×(-2 )=-
)=-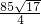 ,
,∴A=
 (100
(100 -
-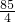
 )=
)= (403-85
(403-85 ),
),即
 =
= (403-85
(403-85 ).
).分析:由题可得:α+β=7,αβ=8,则α2+β2=(α+β)2-2αβ=33,(α-β)2=(α+β)2-4αβ=17,而α>β,则α-β=
 ,设A=
,设A=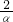 +3β2,B=
+3β2,B=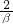 +3,求出A+B及A-B即可得出答案.
+3,求出A+B及A-B即可得出答案.点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a,b是方程x2-2x-1=0的两个根,则a2+a+3b的值是( )
| A、7 | ||
| B、-5 | ||
C、7
| ||
| D、-2 |