题目内容
12.抛物线y=3x2,y=3x2-2,y=$\frac{1}{3}$x2+1共有的性质是( )| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 都有最高点 | D. | y随x的增大而增大 |
分析 根据二次函数的性质:开口方向、对称轴以及增减性逐一分析探讨得出答案即可.
解答 解:y=3x2开口向上,对称轴为y轴,有最低点,顶点为原点;
y=3x2-2开口向上,对称轴为y轴,有最低点,顶点为(0,-2);
y=$\frac{1}{3}$x2+1开口向上,对称轴为y轴,有最低点,顶点为(0,1).
故选:B.
点评 此题考查二次函数的性质,掌握二次函数顶点式y=a(x-h)2+k的性质是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.二次函数y=x2-3x+2的图象与x轴的两个交点坐标是( )
| A. | 1和2 | B. | -1和-2 | C. | (-1,0)和(-2,0) | D. | (1,0)和(2,0) |
4.圆、平行四边形、等腰三角形、菱形,矩形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
1.若(x-1)0=1,求x的取值范围( )
| A. | x≤1 | B. | x≥1 | C. | x≠1 | D. | x=1 |
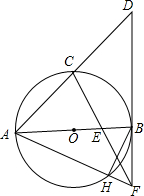 如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,连结AC并延长到点D,使AC=CD,E是OB的中点,连结CE并延长交DB于点F.
如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,连结AC并延长到点D,使AC=CD,E是OB的中点,连结CE并延长交DB于点F.