题目内容
已知如图,直线y=ax+b与反比例函数y=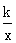 (x<0)的图象相交于点A和点B,与x轴交于点C,其中A点的坐标为(-2,4),点B的横坐标为-4。
(x<0)的图象相交于点A和点B,与x轴交于点C,其中A点的坐标为(-2,4),点B的横坐标为-4。
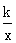 (x<0)的图象相交于点A和点B,与x轴交于点C,其中A点的坐标为(-2,4),点B的横坐标为-4。
(x<0)的图象相交于点A和点B,与x轴交于点C,其中A点的坐标为(-2,4),点B的横坐标为-4。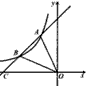
(1)试确定反比例函数的解析式;
(2)求△AOC的面积。
(2)求△AOC的面积。
解:(1)∵反比例函数y=k/x(x<0)的图象过点A(-2,4),
∴k=-8,
∴所求的反比例函数的解析式为y=-8/x;
(2)∵反比例函数y=-8/x(x<0)的图象过点B,且点B的横坐标为-4,
∴点B的纵坐标为2,即点B的坐标为(-4,2),
∵直线y=ax+b过点A(-2,4)、B(-4,2),
∴ 解得
解得 ,
,
∴直线AB的解析式为y=x+6
此时点C的坐标为(-6,0),
∴△AOC的面积S△AOC=1/2×6×4=12。
∴k=-8,
∴所求的反比例函数的解析式为y=-8/x;
(2)∵反比例函数y=-8/x(x<0)的图象过点B,且点B的横坐标为-4,
∴点B的纵坐标为2,即点B的坐标为(-4,2),
∵直线y=ax+b过点A(-2,4)、B(-4,2),
∴
 解得
解得 ,
,∴直线AB的解析式为y=x+6
此时点C的坐标为(-6,0),
∴△AOC的面积S△AOC=1/2×6×4=12。

练习册系列答案
相关题目
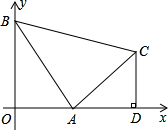 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D. 已知如图,直线y=-
已知如图,直线y=- 已知如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于h,若正方形ABCD的四个顶点分别在四条直线上,求它的面积.
已知如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于h,若正方形ABCD的四个顶点分别在四条直线上,求它的面积. 已知如图:直线AB、CD被l所截,AB∥CD,EF平分∠CEG,GH平分∠BGE.求证:EF∥GH.
已知如图:直线AB、CD被l所截,AB∥CD,EF平分∠CEG,GH平分∠BGE.求证:EF∥GH. 已知如图,直线AB、CD相交于O,∠AOC=50°,OE平分∠DOB,求∠COE的度数.
已知如图,直线AB、CD相交于O,∠AOC=50°,OE平分∠DOB,求∠COE的度数.