Question

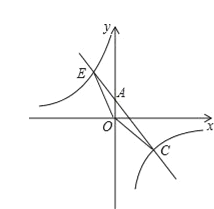
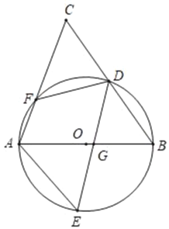
【题目】如图，AB是⊙O的直径，D，E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD＝BD，连接AC交⊙O于点F，连接AE，DE，DF．

（1）证明：∠E＝∠C；

（2）若∠E＝55°，求∠BDF的度数．

Answer 1

【答案】（1）详见解析；（2）110°．

【解析】

（1）连接AD，利用直径所对的圆周角为直角，可得AD⊥BC，再根据CD＝BD，故AD垂直平分BC，根据垂直平分线上的点到线段两个端点的距离相等，可得：AB＝AC，再根据等边对等角和同弧所对的圆周角相等即可得到∠E＝∠C；

（2）根据内接四边形的性质：四边形的外角等于它的内对角，可得∠CFD＝∠E＝55°，再利用外角的性质即可求出∠BDF.

（1）证明：连接AD，如图所示：

∵AB是⊙O的直径，

∴∠ADB＝90°，即AD⊥BC，

∵CD＝BD，

∴AD垂直平分BC，

∴AB＝AC，

∴∠B＝∠C，

∵∠B＝∠E，

∴∠E＝∠C；

（2）解：∵四边形AEDF是⊙O的内接四边形，

∴∠AFD＝180°﹣∠E，

∵∠CFD＝180°﹣∠AFD，

∴∠CFD＝∠E＝55°，

由（1）得：∠E＝∠C＝55°，

∴∠BDF＝∠C+∠CFD＝55°+55°＝110°．