题目内容
5.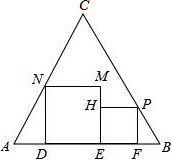 如图,正三角形ABC的边长为3+$\sqrt{3}$,在正三角形ABC中放入正方形DEMN和EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,这两个正方形面积和的最小值是$\frac{9}{2}$,最大值是99-54$\sqrt{3}$.
如图,正三角形ABC的边长为3+$\sqrt{3}$,在正三角形ABC中放入正方形DEMN和EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,这两个正方形面积和的最小值是$\frac{9}{2}$,最大值是99-54$\sqrt{3}$.
分析 设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,根据等边三角形的性质得∠A=∠B=60°,AB=3+$\sqrt{3}$,利用含30度的直角三角形三边的关系得AD=$\frac{\sqrt{3}}{3}$DN=$\frac{\sqrt{3}}{3}$m,BF=$\frac{\sqrt{3}}{3}$PF=$\frac{\sqrt{3}}{3}$n,则$\frac{\sqrt{3}}{3}$m+m+n+$\frac{\sqrt{3}}{3}$n=3+$\sqrt{3}$,所以n=3-m,S=m2+n2=m2+(3-m)2=2(m-$\frac{3}{2}$)2+$\frac{9}{2}$,接着确定m的取值范围为6$\sqrt{3}$-9≤m≤3$\sqrt{3}$-3,然后根据二次函数的性质求出S的最小和最大值.
解答 解:设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,
∵△ABC为等边三角形,
∴∠A=∠B=60°,AB=3+$\sqrt{3}$,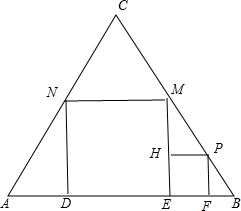
在Rt△ADN中,AD=$\frac{\sqrt{3}}{3}$DN=$\frac{\sqrt{3}}{3}$m,
在Rt△BPF中,BF=$\frac{\sqrt{3}}{3}$PF=$\frac{\sqrt{3}}{3}$n,
∵AD+DE+EF+BF=AB,
∴$\frac{\sqrt{3}}{3}$m+m+n+$\frac{\sqrt{3}}{3}$n=3+$\sqrt{3}$,
∴m+n=3,
∴n=3-m,
∴S=m2+n2=m2+(3-m)2=2(m-$\frac{3}{2}$)2+$\frac{9}{2}$
当点M落在BC上,则正方形DEMN的边长最小,正方形EFPH的边长最大,如图,
在在Rt△ADN中,AD=$\frac{\sqrt{3}}{3}$DN,AN=$\frac{2\sqrt{3}}{3}$DN,
∴DN+$\frac{2\sqrt{3}}{3}$DN=3+$\sqrt{3}$,解得DN=3$\sqrt{3}$-3,
在Rt△BPF中,BF=$\frac{\sqrt{3}}{3}$PF,
∴$\frac{\sqrt{3}}{3}$(3$\sqrt{3}$-3)+3$\sqrt{3}$-3+EF+$\frac{\sqrt{3}}{3}$PF=3+$\sqrt{3}$,解得PF=6$\sqrt{3}$-9,
∴6$\sqrt{3}$-9≤m≤3$\sqrt{3}$-3,
∴当m=$\frac{3}{2}$时,S最小,S的最小值为$\frac{9}{2}$;当m=3$\sqrt{3}$-3时,S最大,S的最大值=2(3$\sqrt{3}$-3-$\frac{3}{2}$)2+$\frac{9}{2}$=99-54$\sqrt{3}$.
故答案为$\frac{9}{2}$;99-54$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;利用相似比计算相应线段的长.也考查了正方形的性质、等边三角形的性质和二次函数的性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 有4个单项式,2个多项式 | B. | 有4个单项式,3个多项式 | ||
| C. | 有7个整式 | D. | 有3个单项式,2个多项式 |
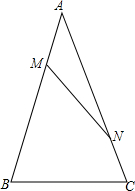 如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.
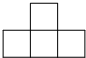
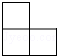
如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.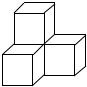 如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )
如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )


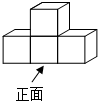 如图是由四个大小相同的正方体搭成的几何体,则它的主视图是( )
如图是由四个大小相同的正方体搭成的几何体,则它的主视图是( )