题目内容
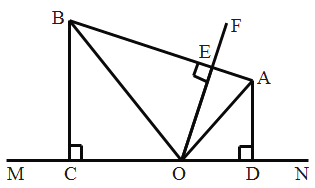
【题目】如图所示,点![]() 分别是
分别是![]() 平分线上的点,
平分线上的点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,下列结论错误的是( )
,下列结论错误的是( )
A.![]()
B.![]()
C.点![]() 是
是![]() 的中点
的中点
D.图中与![]() 互余的角有两个
互余的角有两个
【答案】D
【解析】
根据角分线的定义,可证![]() ;
;
根据角平分线上的点到角两边距离相等可证![]() ;
;
通过证明![]() 和
和![]() 可得OD=OE=OC;
可得OD=OE=OC;
通过同角或等角的余角相等,可证明与![]() 互余的角有四个.由此可判断.
互余的角有四个.由此可判断.
解:∵点A,B分别是∠NOF,∠MOF平分线上的点
∴![]()
∴![]()
即![]() ,故A正确;
,故A正确;
又∵![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]()
∴![]()
∴![]() ,故B选项正确;
,故B选项正确;
在Rt△AOD和Rt△AOE中,
![]()
∴![]()
∴OD=OE,∠OAE=∠OAD
同理可证OC=OE
∴OC= OD,即O为CD的中点,故C正确;
∵![]() 于点
于点![]() ,
,
∴∠COB+∠CBO=90°,
又∵![]() ,
,
∴∠BOE+∠CBO=90°,
∵![]() ,
,![]() 于点
于点![]()
∴∠BOE+∠AOE=90°,∠OAE+∠AOE=90°
∴∠BOE=∠OAE=∠OAD
∴∠OAE +∠CBO=90°,∠OAD +∠CBO=90°
所以与∠CBO互余的角有四个,分别为∠COB,∠BOE,∠OAE,∠OAD,D选项错误;
故选D.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目