题目内容
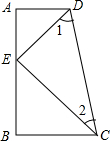 已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
解:∵CE平分∠BCD,DE平分∠CDA,
∴∠1= ∠ADC,∠2=
∠ADC,∠2= ∠BCD,
∠BCD,
∴∠1+∠2= ∠ADC+
∠ADC+ ∠BCD=
∠BCD= (∠ADC+∠BCD)=90°,
(∠ADC+∠BCD)=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴∠A+∠B=180°,
∵CB⊥AB,
∴∠A=90°,
∴DA⊥AB.
分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2= (∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
点评:此题考查了平行线的性质与判定.注意平行线的性质与判定的综合应用,关键是证出AD∥BC.
∴∠1=
 ∠ADC,∠2=
∠ADC,∠2= ∠BCD,
∠BCD,∴∠1+∠2=
 ∠ADC+
∠ADC+ ∠BCD=
∠BCD= (∠ADC+∠BCD)=90°,
(∠ADC+∠BCD)=90°,∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴∠A+∠B=180°,
∵CB⊥AB,
∴∠A=90°,
∴DA⊥AB.
分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2=
 (∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.点评:此题考查了平行线的性质与判定.注意平行线的性质与判定的综合应用,关键是证出AD∥BC.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 19、已知:如图 AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.
19、已知:如图 AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数. 已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.
已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD. 已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
