题目内容
4．
△ABC在平面直角坐标系xOy中的位置如图所示（1）作△ABC关于原点O成中心对称的△A1B1C1，并写出A1B1C1的坐标．
（2）画出△ABC绕点B顺时针旋转90°所得的△A2B2C2．
分析 （1）根据关于原点中心对称的点的坐标特征，分别描出点A、B、C的对应点A1、B1、C1，即可得到△A1B1C1；
（2）利用网格特点，根据旋转的性质画出点A、B旋转后的对应点A2、C2，即可得到△A2BC2．
解答 解：①如图，△A1B1C1为所作，A1（2，-3），B1（1，-1），C1（0，-2）；
②如图，△A2BC2为所作．
点评 本题考查了作图-旋转变换，根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
练习册系列答案
相关题目
12．
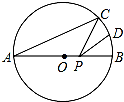如图，AB是⊙O的直径，AB=2，点C在⊙O上，∠CAB=30°，D为弧BC的中点，P是直径AB上一动点，则PC+PD的最小值为（ ）
如图，AB是⊙O的直径，AB=2，点C在⊙O上，∠CAB=30°，D为弧BC的中点，P是直径AB上一动点，则PC+PD的最小值为（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | 1 | D． | 2 |
9．数据：-2，-1，0，1，2的平均数是（ ）
| A． | -2 | B． | -1 | C． | 0 | D． | 6 |
如图，方格纸上画有两条线段，请再画1条线段，使图中的3条线段组成一个轴对称图形（找出符合条件的所有线段）．
13．
如图所示的正六棱柱，不是正六棱柱三视图的是（ ）
如图所示的正六棱柱，不是正六棱柱三视图的是（ ）| A． |  | B． |  | C． |  | D． |  |