题目内容
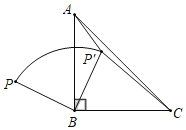
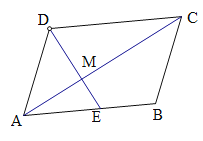
【题目】（操作、填空）如图，
中，对角线
，点
是边
上一动点，连接
交
于点
.
（1）若
，则
的长为 ；（用含
的式子表示，下同）
（2）若
，则的长为 ；
（3）若
，则的长为 ；
……
（猜想、论证）若
，请用含
，的式子表示，并证明结论的正确性.
【答案】操作、填空（1）
；（2）
；（3）
；猜想、论证
，证明详见解析.
【解析】
操作、填空：（1）（2）（3）证明
∽
，利用相似三角形的性质即可求出
的长；
猜想、论证：证明∽，利用相似三角形的性质即可求出的长.
操作、填空
（1）∵
∴
∵
∴
∴
∵
∴∽
∴
又∵AM+CM=AC=a
∴
；
（2）∵
∴
∵
∴
∴
∵
∴∽
∴
又∵AM+CM=AC=a
∴
；
（3）∵
∴
∵
∴
∴
∵
∴∽
∴
又∵AM+CM=AC=a
∴
；
猜想、论证
证明：∵
∴
∵
∴
∴
∵
∴∽
∴
∴
故结论正确.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
