题目内容
12.若m=$\frac{2015}{\sqrt{2016}-1}$,则m5-m4-2015m3=$(\sqrt{2016}+1)^{4}$.分析 先对m进行化简,然后代入所求的式子即可解答本题.
解答 解:∵m=$\frac{2015}{\sqrt{2016}-1}$,
∴$m=\frac{2015×(\sqrt{2016}+1)}{(\sqrt{2016}-1)(\sqrt{2016}+1)}=\frac{2015×(\sqrt{2016}+1)}{2015}$=$\sqrt{2016}+1$,
∴m5-m4-2015m3
=m3(m2-m-2015)
=$(\sqrt{2016}+1)^{3}[(\sqrt{2016}+1)^{2}-(\sqrt{2016}+1)-2015]$
=$(\sqrt{2016}+1)^{3}[2016+2\sqrt{2016}+1-\sqrt{2016}-1-2015]$
=$(\sqrt{2016}+1)^{3}(\sqrt{2016}+1)$
=$(\sqrt{2016}+1)^{4}$.
故答案为:$(\sqrt{2016}+1)^{4}$.
点评 本题考查二次根式的化简求值,解题的关键是对二次根式的化简,注意在化简过程中要认真,分母如果是无理式要进行分母有理化.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
3.P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
7.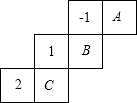 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )| A. | -1,-2,1 | B. | -1,1,-2 | C. | -2,-1,1 | D. | 1,-1,-2 |
 如图所示,长方形的长为a,宽为b,写出计算阴影部分的面积S的公式;当a=3,b=2时,求S的值.
如图所示,长方形的长为a,宽为b,写出计算阴影部分的面积S的公式;当a=3,b=2时,求S的值.