题目内容
 如图,已知点A的坐标为(
如图,已知点A的坐标为( ,3),AB⊥x轴,垂足为B,连接OA,反比例函数
,3),AB⊥x轴,垂足为B,连接OA,反比例函数 (k>0)的图象与线段OA、AB分别交于点C、D,若AB=3BD.
(k>0)的图象与线段OA、AB分别交于点C、D,若AB=3BD.
(1)求点C的坐标;
(2)以点C为圆心,CA的 倍的长为半径作圆,试判断该圆与x轴的位置关系.
倍的长为半径作圆,试判断该圆与x轴的位置关系.
解:(1)∵A( ,3),AB=3BD,
,3),AB=3BD,
∴D( ,1),
,1),
∵点D在反比例函数y= 的图象上,
的图象上,
∴k= ,
,
∴反比例函数的解析式为y= ,
,
设直线OA的解析式为y=kx(k≠0),则3= k,解得k=
k,解得k= ,
,
∴直线OA的解析式为y= x,
x,
∴ ,
,
解得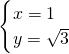 或
或 (舍去),
(舍去),
∴C(1, );
);
 (2)过C点做CE垂直于OB于点E,
(2)过C点做CE垂直于OB于点E,
∵A( ,3),C(1,
,3),C(1, ),
),
∴AC= =2
=2 ,
,
∵C(1, ),
),
∴OC=2,
∴CA=2 -2,
-2,
∴ CA=
CA= (
( -1),CE=
-1),CE= ,
,
∵ (
( -1)-
-1)- =
= -
- >0,
>0,
∴该圆与x轴相交.
分析:(1)先根据A( ,3),AB=3BD求出D点坐标,进而可得出反比例函数y=
,3),AB=3BD求出D点坐标,进而可得出反比例函数y= 的解析式,用待定系数法求出直线OA的解析式,求出直线与反比例函数的交点坐标即可;
的解析式,用待定系数法求出直线OA的解析式,求出直线与反比例函数的交点坐标即可;
(2)过C点做CE垂直于OB于点E,由A、C两点的坐标求出AC的长,根据C点坐标得出OC的长,进而得出CA的长,再比较出 CA与CE长度的大小即可.
CA与CE长度的大小即可.
点评:本题考查的是反比例函数综合题,涉及到用待定系数法求一次函数及反比例函数的解析式等知识,难度适中.
 ,3),AB=3BD,
,3),AB=3BD,∴D(
 ,1),
,1),∵点D在反比例函数y=
 的图象上,
的图象上,∴k=
 ,
,∴反比例函数的解析式为y=
 ,
,设直线OA的解析式为y=kx(k≠0),则3=
 k,解得k=
k,解得k= ,
,∴直线OA的解析式为y=
 x,
x,∴
 ,
,解得
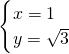 或
或 (舍去),
(舍去),∴C(1,
 );
); (2)过C点做CE垂直于OB于点E,
(2)过C点做CE垂直于OB于点E,∵A(
 ,3),C(1,
,3),C(1, ),
),∴AC=
 =2
=2 ,
,∵C(1,
 ),
),∴OC=2,
∴CA=2
 -2,
-2,∴
 CA=
CA= (
( -1),CE=
-1),CE= ,
,∵
 (
( -1)-
-1)- =
= -
- >0,
>0,∴该圆与x轴相交.
分析:(1)先根据A(
 ,3),AB=3BD求出D点坐标,进而可得出反比例函数y=
,3),AB=3BD求出D点坐标,进而可得出反比例函数y= 的解析式,用待定系数法求出直线OA的解析式,求出直线与反比例函数的交点坐标即可;
的解析式,用待定系数法求出直线OA的解析式,求出直线与反比例函数的交点坐标即可;(2)过C点做CE垂直于OB于点E,由A、C两点的坐标求出AC的长,根据C点坐标得出OC的长,进而得出CA的长,再比较出
 CA与CE长度的大小即可.
CA与CE长度的大小即可.点评:本题考查的是反比例函数综合题,涉及到用待定系数法求一次函数及反比例函数的解析式等知识,难度适中.

练习册系列答案
相关题目
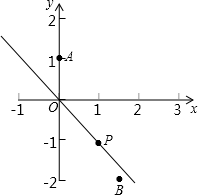 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
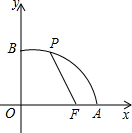 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-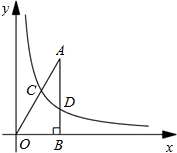 如图,已知点A的坐标为(
如图,已知点A的坐标为(

 如图,已知点A的坐标为(
如图,已知点A的坐标为(